Perturbative Neural Networks (PNN)
This is an attempt to reproduce results in Perturbative Neural Networks paper. See original repo for details.
Motivation
The original implementation used regular convolutions in the first layer, and the remaining layers used fanout of 1, which means each input channel was perturbed with a single noise mask.
However, the biggest issue with the original implementation is that test accuracy was calculated incorrectly. Instead of the usual method of calculating ratio of correct samples to total samples in the test dataset, the authors calculated accuracy on per batch basis, and applied smoothing weight (test_accuracy = 0.7 * prev_batch_accuracy + 0.3 * current_batch_accuracy).
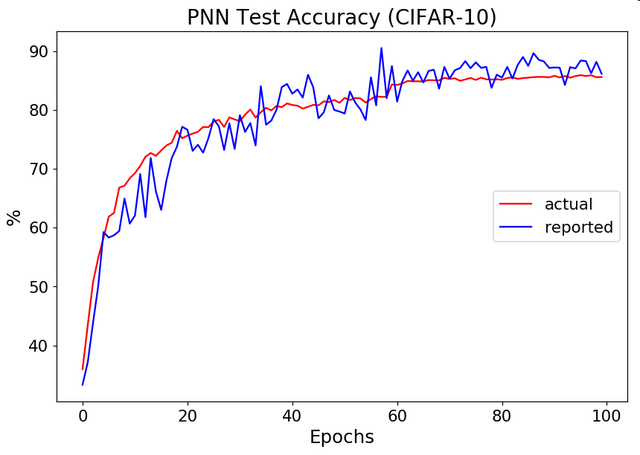
Here's how this method (reported) compares to the proper accuracy calculation (actual):
For this model run (noiseresnet18 on CIFAR10), the code in original repo would report best test accuracy 90.53%, while the actual best test accuracy is 85.91%
After correcting this issue, I ran large number of experiments trying to see if perturbing input with noise masks would provide any benefit, and my conclusion is that it does not.
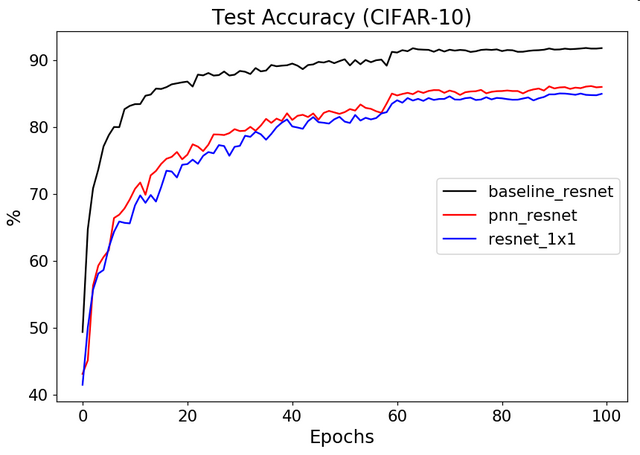
Here's for example, the difference between ResNet18-like models: a baseline model with reduced number of filters to keep the same parameter count, a model where all layers except first one use only 1x1 convolutions (no noise), and a model where all layers except first one use perturbations followed by 1x1 convolutions. All three models have ~5.5M parameters:
The accuracy difference between regular resnet baseline and PNN remains ~5% throughout the training, and the addition of noise masks results in less than 1% improvement over equivalently "crippled" resnet without any noise applied.
Implementation details
Most of the modifications are contained in the PerturbLayer class. Here are the main changes from the original code:
--first_filter_size and --filter_size arguments control the type of the first layer, and the remaining layers, correspondingly. A value of 0 turns the layer into a perturbation layer, as described in the paper. Any value n > 0 will turn the layer into a regular convolutional layer with filter size n. The original implementation only supports first_filter_size=7, and filter_size=0.
--nmasks specifies number of noise masks to apply to each input channel. This is "fanout" parameter mentioned in the paper. The original implementation only supports nmasks=1.
--unique_masks specifies whether to use different sets of nmasks noise masks for each input channel. --no-unique_masks forces the same set of nmasks to be used for all input channels.
--train_masks enables treating noise masks as regular parameters, and optimizes their values during training at the same time as model weights.
--mix_maps adds second 1x1 convolutional layer after perturbed input channels are combined with the first 1x1 convolution. Without this second 1x1 "mixing" layer, there is no information exchange between input channels all the way until the softmax layer in the end. Note that it's not needed when --nmasks is 1, because then the first 1x1 convolutional layer already plays this role.
Other arguments allow changing noise type (uniform or normal), pooling type (max or avg), activation function (relu, rrelu, prelu, elu, selu, tanh, sigmoid), whether to apply activation function in the first layer (--use_act, immediately after perturbing the input RGB channels, this results in some information loss), whether to scale noise level in the first layer, and --debug argument prints out values of input, noise, and output for every update step to verify that noise is being applied correctly.
Three different models are supported: perturb_resnet18, cifarnet (6 conv layers, followed by a fully connected layer), and lenet (3 conv. layers followed by a fully connected layer). In addition, I included the baseline ResNet-18 model resnet18 taken from here, and noiseresnet18 model from the original repo. Note that perturb_resnet18 model is flexible enough to replace both baseline and noiseresnet18 models, using appropriate arguments.
Results
CIFAR-10:
- Baseline (regular ResNet18 with 3x3 convolutions, number of filters reduced to match PNN parameter count) Test Accuracy: 91.8%
python main.py --net-type 'resnet18' --dataset-test 'CIFAR10' --dataset-train 'CIFAR10' --nfilters 44 --batch-size 10 --learning-rate 1e-3
- Original implementation (equivalent to running the code from the original repo). Test Accuracy: 85.7%
python main.py --net-type 'noiseresnet18' --dataset-test 'CIFAR10' --dataset-train 'CIFAR10' --nfilters 128 --batch-size 10 --learning-rate 1e-4 --first_filter_size 7
-
Same as above, but changing
first_filter_sizeargument to 3 improves the accuracy to 86.2% -
Same as above, but without any noise (resnet18 with 3x3 convolutions in the first layer, and 1x1 in remaining layers). Test Accuracy: 85.5%
python main.py --net-type 'perturb_resnet18' --dataset-test 'CIFAR10' --dataset-train 'CIFAR10' --nfilters 128 --batch-size 16 --learning-rate 1e-3 --first_filter_size 3 --filter_size 1
- PNN with all uniform noise in all layers (including the first layer). Test Accuracy: 72.6%
python main.py --net-type 'perturb_resnet18' --dataset-test 'CIFAR10' --dataset-train 'CIFAR10' --nfilters 128 --batch-size 16 --learning-rate 1e-3 --first_filter_size 0 --filter_size 0 --nmasks 1
- PNN with noise masks in all layers except the first layer, which uses regular 3x3 convolutions with fanout=64. Internally fanout is implemented with grouped 1x1 convolutions. Note: --unique_masks arg creates unique set of masks for each input channel, in every layer, and --mix_maps argument which uses extra 1x1 convolutional layer in all perturbation layers. Test Accuracy: 82.7%
python main.py --net-type 'perturb_resnet18' --dataset-test 'CIFAR10' --dataset-train 'CIFAR10' --nfilters 128 --batch-size 16 --learning-rate 1e-3 --first_filter_size 3 --filter_size 0 --nmasks 64 --unique_masks --mix_maps
- Same as above, but with --no-unique_masks argument, which means that the same set of masks is used for each input channel. Test Accuracy: 82.4%
python main.py --net-type 'perturb_resnet18' --dataset-test 'CIFAR10' --dataset-train 'CIFAR10' --nfilters 128 --batch-size 16 --learning-rate 1e-3 --first_filter_size 3 --filter_size 0 --nmasks 64 --no-unique_masks
Experiments 6 and 7 are the closest to what was described in the paper.
- training the noise masks (updated each batch, at the same time as regular model parameters). Test Accuracy: 85.9%
python main.py --net-type 'perturb_resnet18' --dataset-test 'CIFAR10' --dataset-train 'CIFAR10' --nfilters 128 --batch-size 16 --learning-rate 1e-3 --first_filter_size 3 --filter_size 0 --nmasks 64 --no-unique_masks --train_masks
Weakness of reasoning:
Section 3.3: "given the known input x and convolution transformation matrix A, we can always solve for the matching noise perturbation matrix N".
While for any given single input sample PNN might be able to find the weights required to match the output of a CNN, it does not follow that it can find weights to do that for all input samples in the dataset.
Section 3.4: The result of a single convolution operation is represented as a value of the center pixel Xc in a patch X, plus some quantity Nc (a function of filter weights W and the neighboring pixels of Xc): Y = XW = Xc + Nc. The claim is: "Establishing that Nc behaves like additive perturbation noise, will allows us to relate the CNN formulation to the PNN formulation".
Even if Nc statistically behaves like random noise does not mean it can be replaced with random noise. The random noise in PNN does not depend on values of neighboring pixels in the patch, unlike Nc in a regular convolution. PNN layer lacks the main feature extraction property of a regular convolution: it cannot directly match any spatial patterns with a filter.
Conclusion
It appears that perturbing layer inputs with noise does not provide any significant benefit. Simple 1x1 convolutions without noise masks provide similar performance. No matter how we apply noise masks, the accuracy drop resulting from using 1x1 filters is severe (~5% on CIFAR-10 even when not modifying the first layer). The results published by the authors are invalid due to incorrect accuracy calculation method.
![A PyTorch implementation of EventProp [https://arxiv.org/abs/2009.08378], a method to train Spiking Neural Networks](https://github.com/lolemacs/pytorch-eventprop/raw/master/images/forward.png)



