Change-making-problem / Cambio de monedas
Entendiendo el problema
Dada una cantidad de dinero y una lista de denominaciones de monedas, encontrar el número mínimo de monedas (de determinadas denominaciones) que sumen la cantidad de dinero exacta.
Es un subcaso especial del problema de la mochila
Ejemplo 1:
Pagar la cantidad de 10 usando las siguientes monedas [2,3,5,6] Tenemos 7 posibles combinaciones de cambios {2,2,2,2,2}, {2,2,3,3}, {2,2,6}, {2,3,5}, {5,5}
Donde la mejor combinación es {5,5} que usa la menor cantidad de monedas
Consideraciones
- Este problema supone que todas las monedas están disponibles infinitamente.
- Dado el caso donde la cantidad de dinero es 0 el resultado sera una lista vacia [ ]
- Dado el caso donde no es posible pagar la cantidad con las monedas proporcionadas retornar nulo. Ejemplo cantidad=5 monedas[2,4]
Solucion 1
La primera solución contempla todas las posibles combinaciones, podemos implementarla dividiendo en pequeños subproblemas y aplicando recursividad.
Por cada moneda hacemos una resta de la cantidad de dinero menos el valor de la moneda de esta forma obtenemos un punto de inicio de cada combinación y dividimos el problema en subproblemas. Aqui podemos aplicar recursividad y continuar haciendo las restas mientras la cantidad a pagar disminuye y llega a 0, de esta forma obtenemos todas las posibles combinaciones. En esta parte necesitamos hacer una validación para detener la iteración cuando la cantidad llegue a igual o menor que 0 (Si llega a 0 sabemos que es una posible solución).
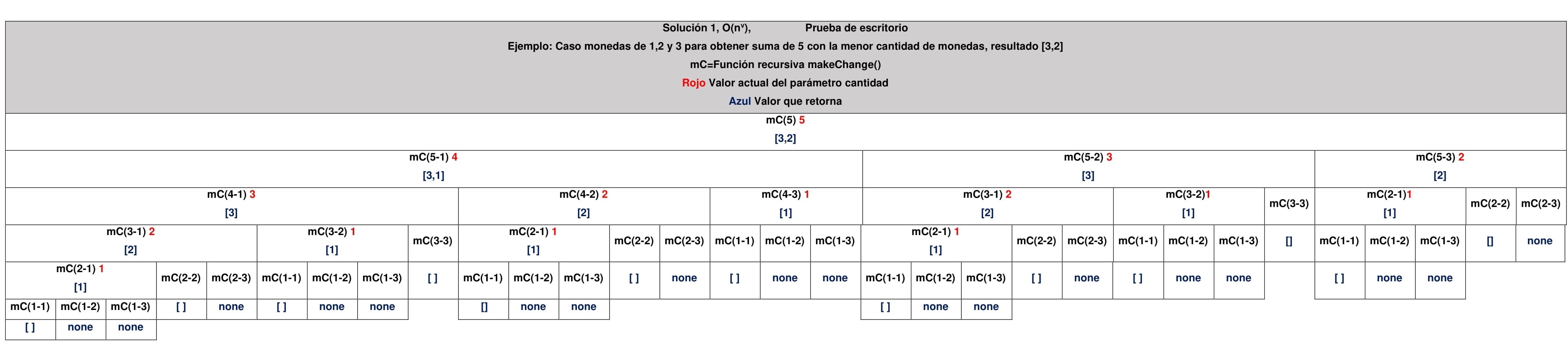
Ejemplo de divición de subproblemas para el caso, monedas: [1,2,3] y cantidad de 5 
Seguido de esto necesitamos encontrar la mejor solución que úse la menor cantidad de monedas, necesitamos hacer una comparacion para obtener la mejor solución de cada suproblema, guardarla y retornar la combinacion con menor cantidad de monedas por cada nivel (cada vez que disminuimos la cantidad a pagar). Por eso esta primera solución es una estrategia de análisis top-down (de arriba hacia abajo)
#monedas debe ser un arreglo de enteros, cantidad debe ser un entero no menor que 0
def makeChange(monedas, cantidad):
if cantidad == 0: #Validación cuando lleguemos a la cantidad 0
return []
if cantidad < 0: #Validación para saber que llegamos a una cantidad negativa que no se puede pagar
return None
resultadoOptimo = None #declaramos e inicializamos el resultadoOptimo que retornaremos
for moneda in monedas: #iteramos sobre cada moneda
#llamamos a makeChange para obtener una posible solución
#Restamos el valor actual de moneda para dividir en subproblemas
combinacion = makeChange(monedas, cantidad - moneda) #Aqui podemos obtener [], None o una posible combinación
if combinacion != None: #Validación para saber que es una posible combinacion
candidata = combinacion + [moneda] #Validación para saber que es una posible combinacion
#Comparamos si la solucion candidata es mejor que el resultadoOptimo actual lo remplazamos
if (resultadoOptimo is None or len(candidata) < len(resultadoOptimo)):
resultadoOptimo = candidata
return resultadoOptimo
Notemos que tenemos subproblemas que se repiten, dada la recursividad y el uso de todas las combinaciones posibles, esta solucion tiene una complejidad exponencial y poco rendimiento.
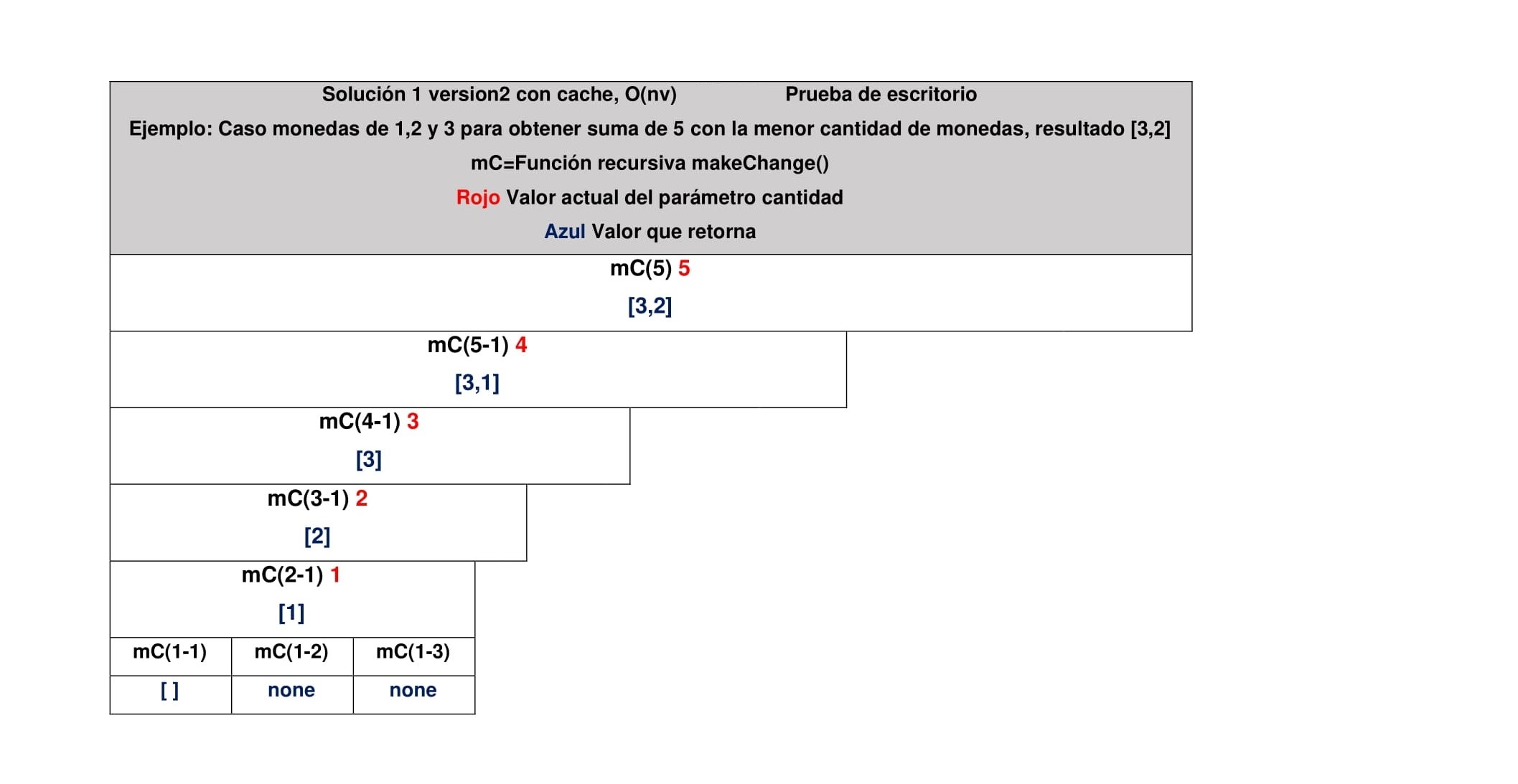
Ejemplo 1/version 2:
Podemos guardar los resultados para reducir la complejidad a O(nv), n es la cantidad de monedas y v la cantidad de pasos, para esto podemos utilizar el módulo functools que nos proporciona un método llamado lru_cache que recibe una función de la cual vamos a poder guardar el resultado o lo que retorna, de esta forma si llamamos a una determinada función con los mismos argunmentos varias veces retornan el valor guardado en memoria sin ejecutar dicha función.
from functools import lru_cache #import del módulo
def makeChange(monedas, cantidad): #Necesitamos una funcion como envolvente para manejar las monedas
@lru_cache(maxsize=None, typed=False) #inicializamos la cache sin límite para la función helper
def helper(cantidad): #Guardamos el resultado para cada cantidad
if cantidad == 0:
return []
if cantidad < 0:
return None
resultadoOptimo = None
for moneda in monedas:
combinacion = helper(cantidad - moneda)
if combinacion != None:
candidata = combinacion + [moneda]
if (resultadoOptimo is None or len(candidata) < len(resultadoOptimo)):
resultadoOptimo = candidata
return resultadoOptimo
return helper(cantidad)
Cada solución es manejada como un módulo, el archivo main.py junta y llama cada solución y calcula su tiempo de ejecución, por defecto maneja el caso de monedas=[1,2,3,4,5,6,7,8,9] y cantidad=20 la cual se puede cambiar en main.py
//with python 3
python main.py
Solucion 2, bottom-up O(nv)
La segunda solución contempla la estrategia de análisis bottom-up, guiandonos de la primera solución empezaremos con la cantidad de 0 agregando las posibles combinaciones de monedas hasta llegar a la cantidad final.