A Python framework for developing parallelized Computational Fluid Dynamics software to solve the hyperbolic 2D Euler equations on distributed, multi-block structured grids.

Related tags

Deep Learning python multiprocessing parallel-computing cfd computational-fluid-dynamics hyperbolic-equations adaptive-mesh-refinement
Overview

Alt Text

pyHype: Computational Fluid Dynamics in Python

pyHype is a Python framework for developing parallelized Computational Fluid Dynamics software to solve the hyperbolic 2D Euler equations on distributed, multi-block structured grids. It can be used as a solver to generate numerical predictions of 2D inviscid flow fields, or as a platform for developing new CFD techniques and methods. Contributions are welcome! pyHype is in early stages of development, I will be updating it regularly, along with its documentation.

The core idea behind pyHype is flexibility and modularity. pyHype offers a plug-n-play approach to CFD software, where every component of the CFD pipeline is modelled as a class with a set interface that allows it to communicate and interact with other components. This enables easy development of new components, since the developer does not have to worry about interfacing with other components. For example, if a developer is interested in developing a new approximate riemann solver technique, they only need to provide the implementation of the FluxFunction abstract class, without having to worry about how the rest of the code works in detail.

NEW: Geometry not alligned with the cartesian axes is now supported!
NEW: 60% efficiency improvement!
COMING UP: Examples of simulations on various airfoil geometries, and a presentation of the newly added mesh optimization techniques.
COMING UP: Examples of simulations on multi-block meshes.

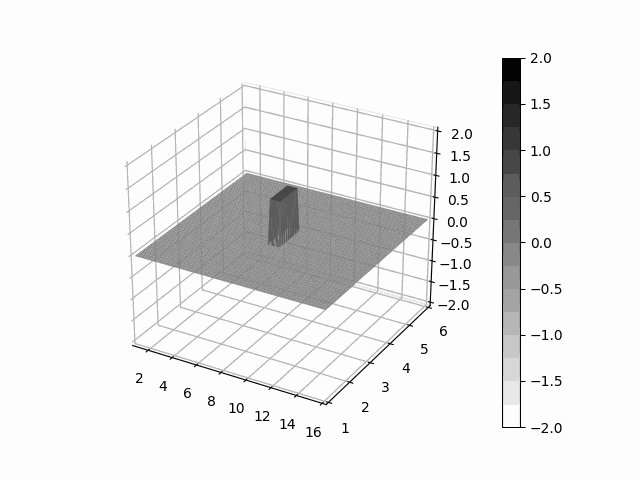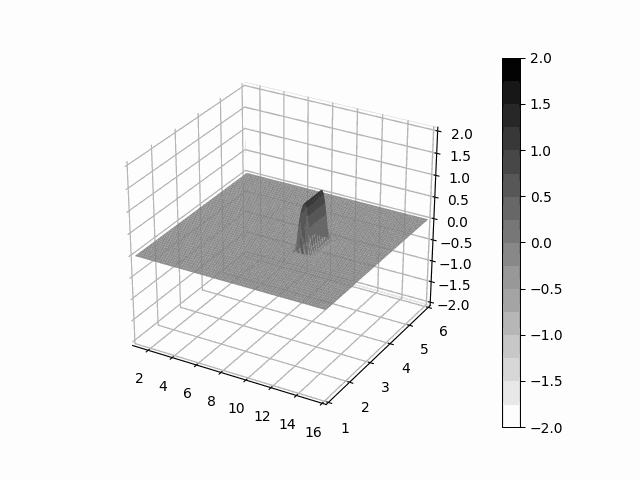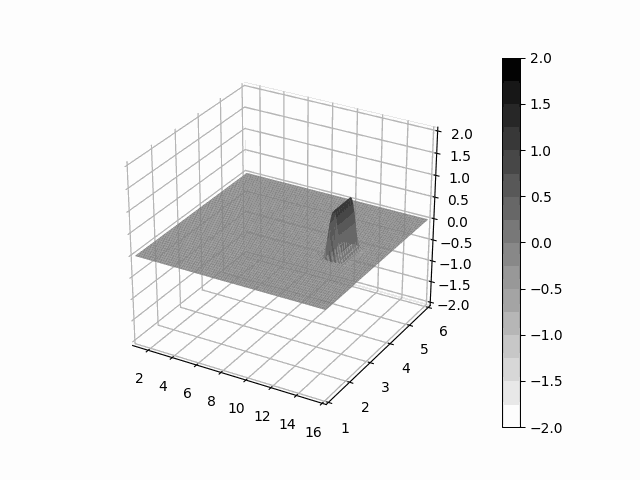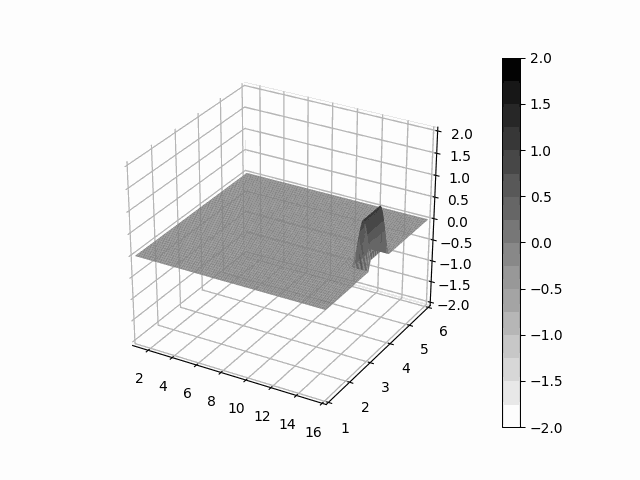
Explosion Simulation

Here is an example of an explosion simulation performed on one block. The simulation was performed with the following:

  • 600 x 1200 cartesian grid
  • Roe approximate riemann solver
  • Venkatakrishnan flux limiter
  • Piecewise-Linear second order reconstruction
  • Green-Gauss gradient method
  • RK4 time stepping with CFL=0.8
  • Reflection boundary conditions

The example in given in the file examples/explosion.py. The file is as follows:

from pyHype.solvers import Euler2D

# Solver settings
settings = {'problem_type':             'explosion',
            'interface_interpolation':  'arithmetic_average',
            'reconstruction_type':      'conservative',
            'upwind_mode':              'primitive',
            'write_solution':           False,
            'write_solution_mode':      'every_n_timesteps',
            'write_solution_name':      'nozzle',
            'write_every_n_timesteps':  40,
            'CFL':                      0.8,
            't_final':                  0.07,
            'realplot':                 False,
            'profile':                  True,
            'gamma':                    1.4,
            'rho_inf':                  1.0,
            'a_inf':                    343.0,
            'R':                        287.0,
            'nx':                       600,
            'ny':                       1200,
            'nghost':                   1,
            'mesh_name':                'chamber'
            }

# Create solver
exp = Euler2D(fvm='SecondOrderPWL',
              gradient='GreenGauss',
              flux_function='Roe',
              limiter='Venkatakrishnan',
              integrator='RK4',
              settings=settings)

# Solve
exp.solve()

alt text

Double Mach Reflection (DMR)

Here is an example of a Mach 10 DMR simulation performed on five blocks. The simulation was performed with the following:

  • 500 x 500 cells per block
  • HLLL flux function
  • Venkatakrishnan flux limiter
  • Piecewise-Linear second order reconstruction
  • Green-Gauss gradient method
  • Strong-Stability-Preserving (SSP)-RK2 time stepping with CFL=0.4

The example in given in the file examples/dmr/dmr.py. The file is as follows:

from pyHype.solvers import Euler2D

# Solver settings
settings = {'problem_type':             'mach_reflection',
            'interface_interpolation':  'arithmetic_average',
            'reconstruction_type':      'conservative',
            'upwind_mode':              'conservative',
            'write_solution':           False,
            'write_solution_mode':      'every_n_timesteps',
            'write_solution_name':      'machref',
            'write_every_n_timesteps':  20,
            'plot_every':               10,
            'CFL':                      0.4,
            't_final':                  0.25,
            'realplot':                 True,
            'profile':                  False,
            'gamma':                    1.4,
            'rho_inf':                  1.0,
            'a_inf':                    1.0,
            'R':                        287.0,
            'nx':                       50,
            'ny':                       50,
            'nghost':                   1,
            'mesh_name':                'wedge_35_four_block',
            'BC_inlet_west_rho':        8.0,
            'BC_inlet_west_u':          8.25,
            'BC_inlet_west_v':          0.0,
            'BC_inlet_west_p':          116.5,
            }

# Create solver
exp = Euler2D(fvm='SecondOrderPWL',
              gradient='GreenGauss',
              flux_function='HLLL',
              limiter='Venkatakrishnan',
              integrator='RK2',
              settings=settings)

# Solve
exp.solve()

alt text

High Speed Jet

Here is an example of high-speed jet simulation performed on 5 blocks. The simulation was performed with the following:

  • Mach 2 flow
  • 100 x 1000 cell blocks
  • HLLL flux function
  • Venkatakrishnan flux limiter
  • Piecewise-Linear second order reconstruction
  • Green-Gauss gradient method
  • RK2 time stepping with CFL=0.4

The example in given in the file examples/jet/jet.py. The file is as follows:

from pyHype.solvers import Euler2D

# Solver settings
settings = {'problem_type':             'subsonic_rest',
            'interface_interpolation':  'arithmetic_average',
            'reconstruction_type':      'primitive',
            'upwind_mode':              'conservative',
            'write_solution':           True,
            'write_solution_mode':      'every_n_timesteps',
            'write_solution_name':      'kvi',
            'write_every_n_timesteps':  20,
            'plot_every':               10,
            'CFL':                      0.4,
            't_final':                  25.0,
            'realplot':                 False,
            'profile':                  False,
            'gamma':                    1.4,
            'rho_inf':                  1.0,
            'a_inf':                    1.0,
            'R':                        287.0,
            'nx':                       1000,
            'ny':                       100,
            'nghost':                   1,
            'mesh_name':                'jet',
            'BC_inlet_west_rho':        1.0,
            'BC_inlet_west_u':          0.25,
            'BC_inlet_west_v':          0.0,
            'BC_inlet_west_p':          2.0 / 1.4,
            }

# Create solver
exp = Euler2D(fvm='SecondOrderPWL',
              gradient='GreenGauss',
              flux_function='HLLL',
              limiter='Venkatakrishnan',
              integrator='RK2',
              settings=settings)

# Solve
exp.solve()

Mach Number: alt text

Density: alt text

Current work

  1. Integrate airfoil meshing and mesh optimization using elliptic PDEs
  2. Compile gradient and reconstruction calculations with numba
  3. Integrate PyTecPlot to use for writing solution files and plotting
  4. Implement riemann-invariant-based boundary conditions
  5. Implement subsonic and supersonic inlet and outlet boundary conditions
  6. Implement connectivity algorithms for calculating block connectivity and neighbor-finding
  7. Create a fully documented simple example to explain usage
  8. Documentation!!

Major future work

  1. Use MPI to distrubute computation to multiple processors
  2. Adaptive mesh refinement (maybe with Machine Learning :))
  3. Interactive gui for mesh design
  4. Advanced interactive plotting
You might also like...
Flow is a computational framework for deep RL and control experiments for traffic microsimulation.
Flow is a computational framework for deep RL and control experiments for traffic microsimulation.

Flow Flow is a computational framework for deep RL and control experiments for traffic microsimulation. See our website for more information on the ap

null 867 Jan 2, 2023
Leibniz is a python package which provide facilities to express learnable partial differential equations with PyTorch
Leibniz is a python package which provide facilities to express learnable partial differential equations with PyTorch

Leibniz is a python package which provide facilities to express learnable partial differential equations with PyTorch

Beijing ColorfulClouds Technology Co.,Ltd. 16 Aug 7, 2022
Official code for Score-Based Generative Modeling through Stochastic Differential Equations
Official code for Score-Based Generative Modeling through Stochastic Differential Equations

Score-Based Generative Modeling through Stochastic Differential Equations This repo contains the official implementation for the paper Score-Based Gen

Yang Song 818 Jan 6, 2023
Code for
Code for "Infinitely Deep Bayesian Neural Networks with Stochastic Differential Equations"

Infinitely Deep Bayesian Neural Networks with SDEs This library contains JAX and Pytorch implementations of neural ODEs and Bayesian layers for stocha

Winnie Xu 95 Nov 26, 2021
Supplementary code for the paper
Supplementary code for the paper "Meta-Solver for Neural Ordinary Differential Equations" https://arxiv.org/abs/2103.08561

Meta-Solver for Neural Ordinary Differential Equations Towards robust neural ODEs using parametrized solvers. Main idea Each Runge-Kutta (RK) solver w

Julia Gusak 25 Aug 12, 2021
PyTorch implementation for SDEdit: Image Synthesis and Editing with Stochastic Differential Equations
PyTorch implementation for SDEdit: Image Synthesis and Editing with Stochastic Differential Equations

SDEdit: Image Synthesis and Editing with Stochastic Differential Equations Project | Paper | Colab PyTorch implementation of SDEdit: Image Synthesis a

null 536 Jan 5, 2023
Partial implementation of ODE-GAN technique from the paper Training Generative Adversarial Networks by Solving Ordinary Differential Equations
Partial implementation of ODE-GAN technique from the paper Training Generative Adversarial Networks by Solving Ordinary Differential Equations

ODE GAN (Prototype) in PyTorch Partial implementation of ODE-GAN technique from the paper Training Generative Adversarial Networks by Solving Ordinary

Somshubra Majumdar 15 Feb 10, 2022
Deep learning library for solving differential equations and more

DeepXDE Voting on whether we should have a Slack channel for discussion. DeepXDE is a library for scientific machine learning. Use DeepXDE if you need

Lu Lu 1.4k Dec 29, 2022
PyTorch implementation for Score-Based Generative Modeling through Stochastic Differential Equations (ICLR 2021, Oral)
PyTorch implementation for Score-Based Generative Modeling through Stochastic Differential Equations (ICLR 2021, Oral)

Score-Based Generative Modeling through Stochastic Differential Equations This repo contains a PyTorch implementation for the paper Score-Based Genera

Yang Song 757 Jan 4, 2023
Comments
  • Dev add corner ghost blocks

    Dev add corner ghost blocks

    • Add JIT version of high order term function for the first order solution gradient object
    • Add a use_JIT parameter to allow the use to switch between functions written using numba JIT or numpy (where applicable).
    • Add some docs to the gradient functions
    opened by momokhalil 0
  • BUG FIX: Fix setting of initial conditions

    BUG FIX: Fix setting of initial conditions

    Fixed some instances where the whole state would be initialized to a single (1, 1, 4) array, instead of broadcasting the (1, 1, 4) array to the full (ny, nx, 4) state array

    opened by momokhalil 0
  • Add documentation and slicers

    Add documentation and slicers

    1. Added slicers for each face (slice arrays for any of the 4 faces)
    2. Added docstrings for flux evaluation functions
    3. rename some functions to make it clear they operate at the quadrature points
    opened by momokhalil 0
  • Add more block base classes, modifications to flux calculations

    Add more block base classes, modifications to flux calculations

    Use reconstructed solution state at block boundaries, either from the interior or the ghost cells, to calculate the boundary states for flux evaluation

    opened by momokhalil 0
Owner
Mohamed Khalil
Machine Learning, Data Science, Computational Fluid Dynamics, Aerospace Engineering
Mohamed Khalil
GitHub
Example-custom-ml-block-keras - Custom Keras ML block example for Edge Impulse

Custom Keras ML block example for Edge Impulse This repository is an example on

Edge Impulse 8 Nov 2, 2022
Code for: Gradient-based Hierarchical Clustering using Continuous Representations of Trees in Hyperbolic Space. Nicholas Monath, Manzil Zaheer, Daniel Silva, Andrew McCallum, Amr Ahmed. KDD 2019.

gHHC Code for: Gradient-based Hierarchical Clustering using Continuous Representations of Trees in Hyperbolic Space. Nicholas Monath, Manzil Zaheer, D

Nicholas Monath 35 Nov 16, 2022
HyperLib: Deep learning in the Hyperbolic space

HyperLib: Deep learning in the Hyperbolic space Background This library implements common Neural Network components in the hypberbolic space (using th

null 105 Dec 25, 2022
PyTorch implementation HoroPCA: Hyperbolic Dimensionality Reduction via Horospherical Projections

HoroPCA This code is the official PyTorch implementation of the ICML 2021 paper: HoroPCA: Hyperbolic Dimensionality Reduction via Horospherical Projec

HazyResearch 52 Nov 14, 2022
Simple Linear 2nd ODE Solver GUI - A 2nd constant coefficient linear ODE solver with simple GUI using euler's method

Simple_Linear_2nd_ODE_Solver_GUI Description It is a 2nd constant coefficient li

:) 4 Feb 5, 2022
Double pendulum simulator using a symplectic Euler's method and Hamiltonian mechanics

Symplectic Double Pendulum Simulator Double pendulum simulator using a symplectic Euler's method. The program calculates the momentum and position of

Scott Marino 1 Jan 12, 2022
Hyperbolic Image Segmentation, CVPR 2022

Hyperbolic Image Segmentation, CVPR 2022 This is the implementation of paper Hyperbolic Image Segmentation (CVPR 2022). Repository structure assets :

Mina Ghadimi Atigh 46 Dec 29, 2022
Python framework for Stochastic Differential Equations modeling

SDElearn: a Python package for SDE modeling This package implements functionalities for working with Stochastic Differential Equations models (SDEs fo

null 4 May 10, 2022
Large Scale Multi-Illuminant (LSMI) Dataset for Developing White Balance Algorithm under Mixed Illumination

Large Scale Multi-Illuminant (LSMI) Dataset for Developing White Balance Algorithm under Mixed Illumination (ICCV 2021) Dataset License This work is l

DongYoung Kim 33 Jan 4, 2023
Time-series-deep-learning - Developing Deep learning LSTM, BiLSTM models, and NeuralProphet for multi-step time-series forecasting of stock price.

Stock Price Prediction Using Deep Learning Univariate Time Series Predicting stock price using historical data of a company using Neural networks for

Abdultawwab Safarji 7 Nov 27, 2022