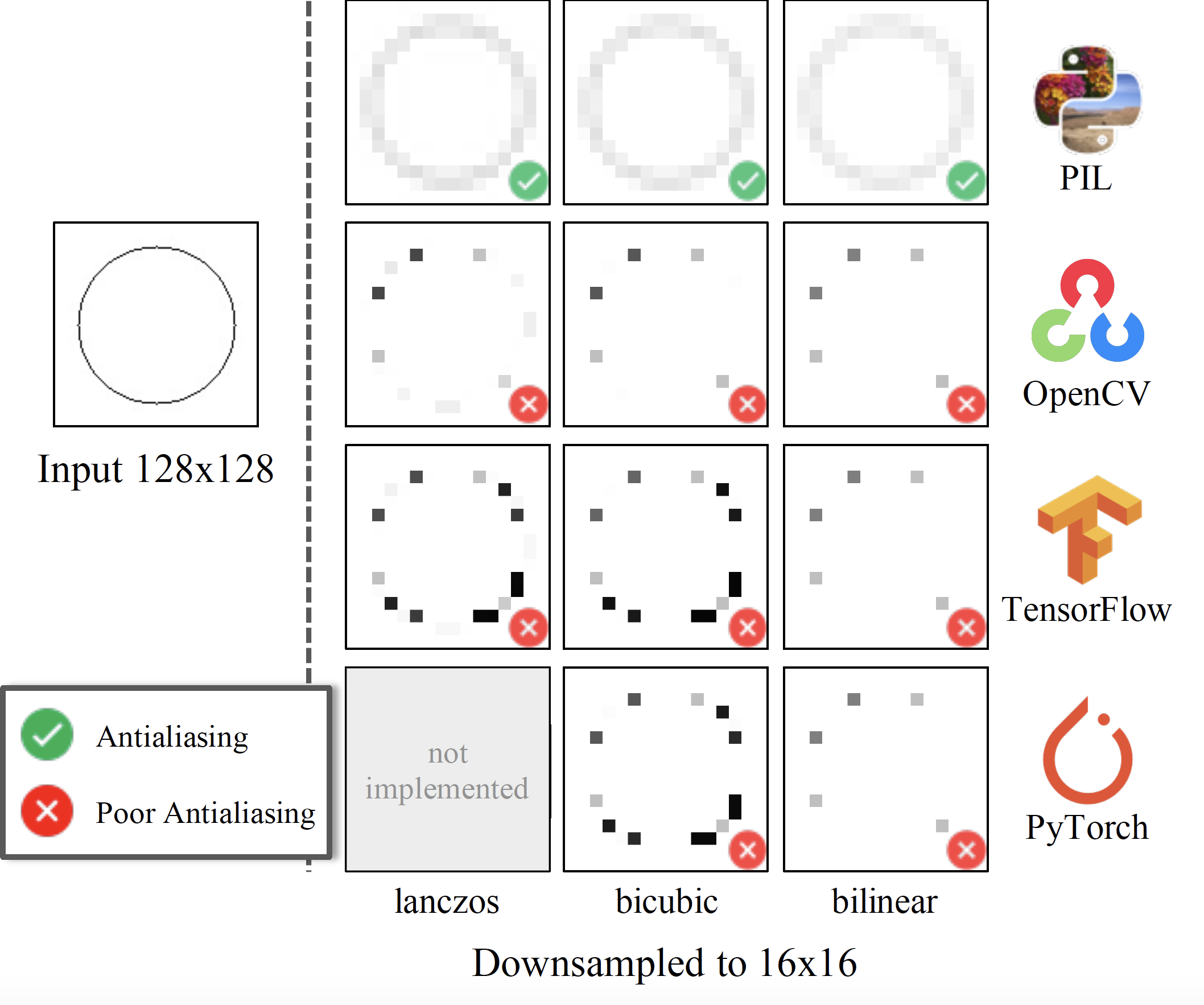
A Criticism of the Paper On Buggy Resizing Libraries
This repository contains:
- a Jupyter notebook for reproducing the aliased image downsampling fenomenon, as demonstrated in the On Buggy Resizing Libraries paper, which argues that the image downsampling methods of the OpenCV, Tensorflow and PyTorch libraries are "buggy", with only PIL being correct.
- simple solutions for antialiasing in every framework, which solves the issue in all cases using the same functions, simply by setting parameters appropriately:
- OpenCV: change the interpolation from bilinear to area (from
cv2.INTER_LINEARtocv2.INTER_AREA) - Tensorflow: set the antialias flag to
True - PyTorch: change the interpolation mode from
bilineartoarea, or simply usetorchvision.transforms.Resize()instead oftorch.nn.functional.interpolate()
- OpenCV: change the interpolation from bilinear to area (from
Try it out in a Colab Notebook:
My opinion:
- neither of the used image downsampling methods is "buggy", not applying antialiasing by default is an understandable design decision for both image and tensor operations.
- the main figure of the paper is misleading, and it only illustrates the issues of aliasing for image resizing.
- the aliasing issue with downsampling can be solved in all frameworks by simply setting a few parameters correctly. My criticism is that this is not mentioned in the paper.
torchvision.transforms.Resize()is claimed to only be a "a wrapper around the PIL library" in a note in Section 3.2 of the paper. This is true for PIL image inputs, but is incorrect fortorch.Tensors, which are resized using torchvision interpolation operations.- the remaining parts of the paper provide valuable insights into the effects of interpolation methods, quantization and compression on the FID score of generative models.
Update: Just found out that there is another, very thorough investigation of the same issue. Highly recommend checking the blogpost out. They also implement an OpenCV-compatible Pillow-equivalent resizing that provides proper antialiasing for all interpolations.