A splitting bijector splits an input x in two equal parts, x1 and x2 (see for instance Glow paper):
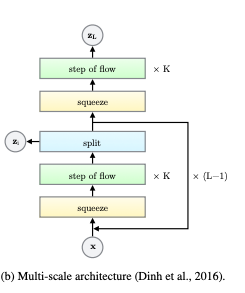
Of those, only x1 is passed to the remaining part of the flow. x2 on the other hand is "normalized" by a location and scale determined by x1.
The transform usually looks like this
def _forward(self, x):
x1, x2 = x.chunk(2, -1)
loc, scale = some_parametric_fun(x1)
x2 = (x2 - loc) / scale
log_abs_det_jacobian = scale.reciprocal().log().sum() # part of the jacobian that accounts for the transform of x2
log_abs_det_jacobian += self.normal.log_prob(x2).sum() # since x2 will disappear, we can include its prior log-lik here
return x1, log_abs_det_jacobian
The _inverse is done like this
def _inverse(self, y):
x1 = y
loc, scale = some_parametric_fun(x1)
x2 = torch.randn_like(x1) # since we fit x2 to a gaussian in forward
log_abs_det_jacobian += self.normal.log_prob(x2).sum()
x2 = x2 * scale + loc
log_abs_det_jacobian = scale.reciprocal().log().sum()
return torch.cat([x1, x2], -1), log_abs_det_jacobian
However, I personally find this coding very confusing:
First and foremost, it messes up with the logic y = flow(x) -> dist.log_prob(y). What if we don't want a normal? That seems orthogonal to the bijector responsibility to me.
Second, it includes in the LADJ a normal log-likelihood, which should come from the prior. Third, it makes the _inverse stochastic, but that should not be the case. Finally, it has an input of -- say -- dimension d and an output of d/2 (and conversely for _inverse).
For some models (e.g. Glow), when generating data, we don't sample from a Gaussian with unit variance but from a Gaussian with some decreased temperature (e.g. an SD of 0.9 or something). With this logic, we'd have to tell every split layer in a flow to modify the self.normal scale!
What I would suggest is this:
we could use SplitBijector as a wrapper around another bijector. The way that would work is this:
class SplitBijector(Bijector):
def __init__(self, bijector):
...
self.bijector = bijector
def _forward(self, x):
x1, x2 = x.chunk(2, -1)
loc, scale = some_parametric_fun(x1)
y2 = (x2 - loc) / scale
log_abs_det_jacobian = scale.reciprocal().log().sum() # part of the jacobian that accounts for the transform of x2
y1 = self.bijector.forward(x1)
log_abs_det_jacobian += self.bijector.log_abs_det_jacobian(x1, y1)
y = torch.cat([y1, y2], 0)
return y, log_abs_det_jacobian
The _inverse would follow.
Of course bijector must have the same input and output space!
That way, we solve all of our problems: input and output space match, no weird stuff happen with a nested normal log-density, the prior density is only called out of the bijector, and one can tweak it at will without caring about what will happen in the bijector.
enhancement


