pm-prophet
Pymc3-based universal time series prediction and decomposition library (inspired by Facebook Prophet). However, while Faceook prophet is a well-defined model, pm-prophet allows for total flexibility in the choice of priors and thus is potentially suited for a wider class of estimation problems.
Table of Contents
Installing pm-prophet
PM-Prophet installation is straightforward using pip: pip install pmprophet
Note that the key dependency of pm-prophet is PyMc3 a library that depends on Theano.
Key Features
- Nowcasting & Forecasting
- Intercept, growth
- Regressors
- Holidays
- Additive & multiplicative seasonality
- Fitting and plotting
- Custom choice of priors (not in Facebook's prophet original model)
- Changepoints in growth
- Automatic changepoint location detection (not in Facebook's prophet original model)
- Fitting with NUTS/AVDI/Metropolis
Experimental warning
⚠️
- Note that automatic changepoint detection is experimental
Differences with Prophet:
- Saturating growth is not implemented
- Uncertainty estimation is different
- All components (including seasonality) need to be explicitly added to the model
- By design pm-prophet places a big emphasis on posteriors and uncertainty estimates, and therefore it won't use MAP for it's estimates.
- While Faceook prophet is a well-defined fixed model, pm-prophet allows for total flexibility in the choice of priors and thus is potentially suited for a wider class of estimation problems
Peyton Manning example
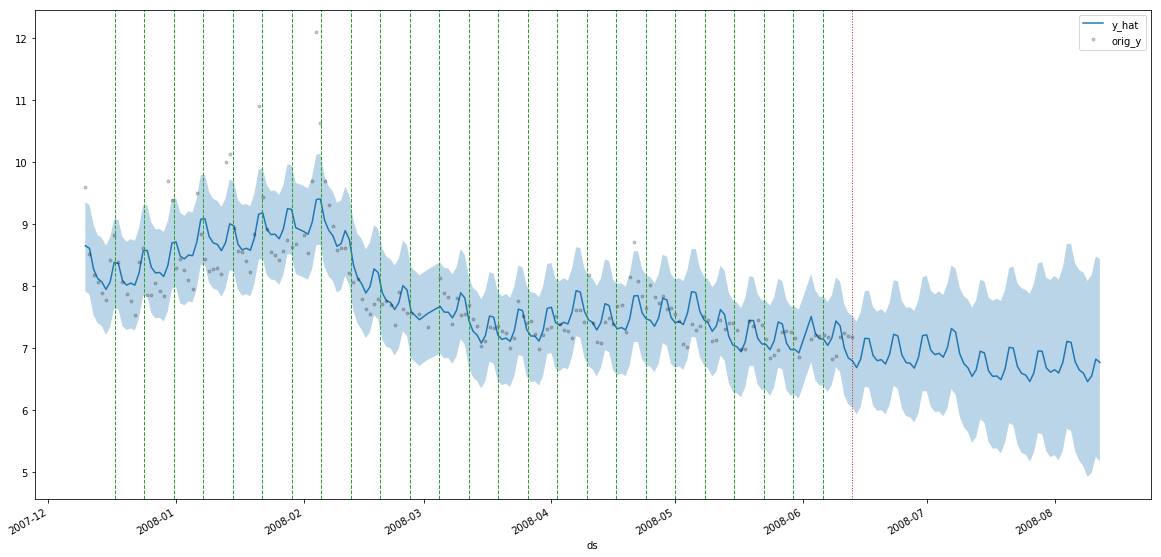
Predicting the Peyton Manning timeseries:
import pandas as pd
from pmprophet.model import PMProphet, Sampler
df = pd.read_csv("examples/example_wp_log_peyton_manning.csv")
df = df.head(180)
# Fit both growth and intercept
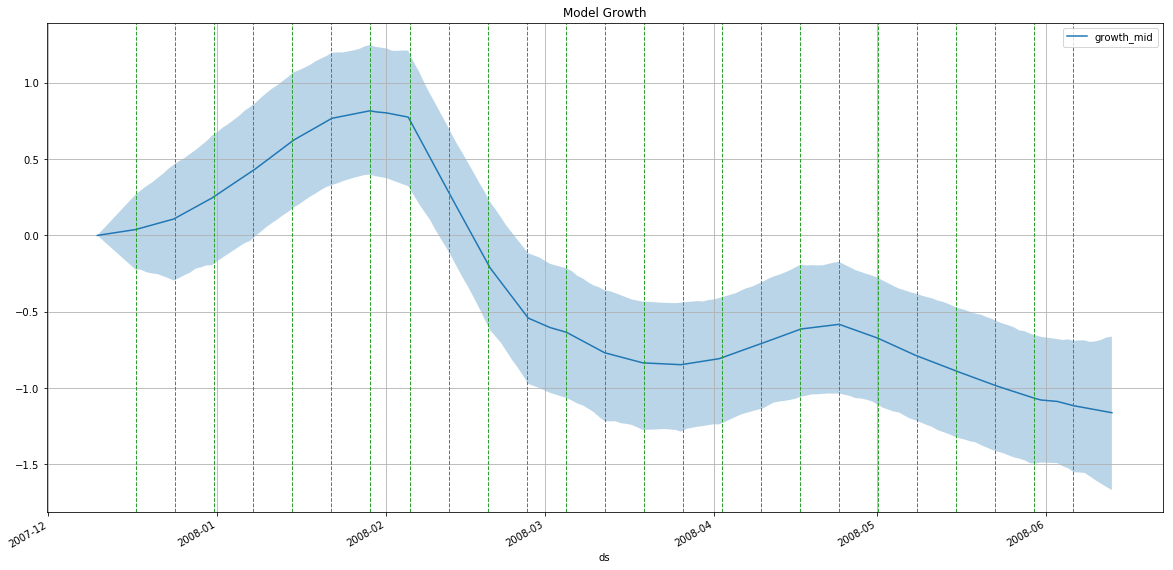
m = PMProphet(df, growth=True, intercept=True, n_changepoints=25, changepoints_prior_scale=.01, name='model')
# Add monthly seasonality (order: 3)
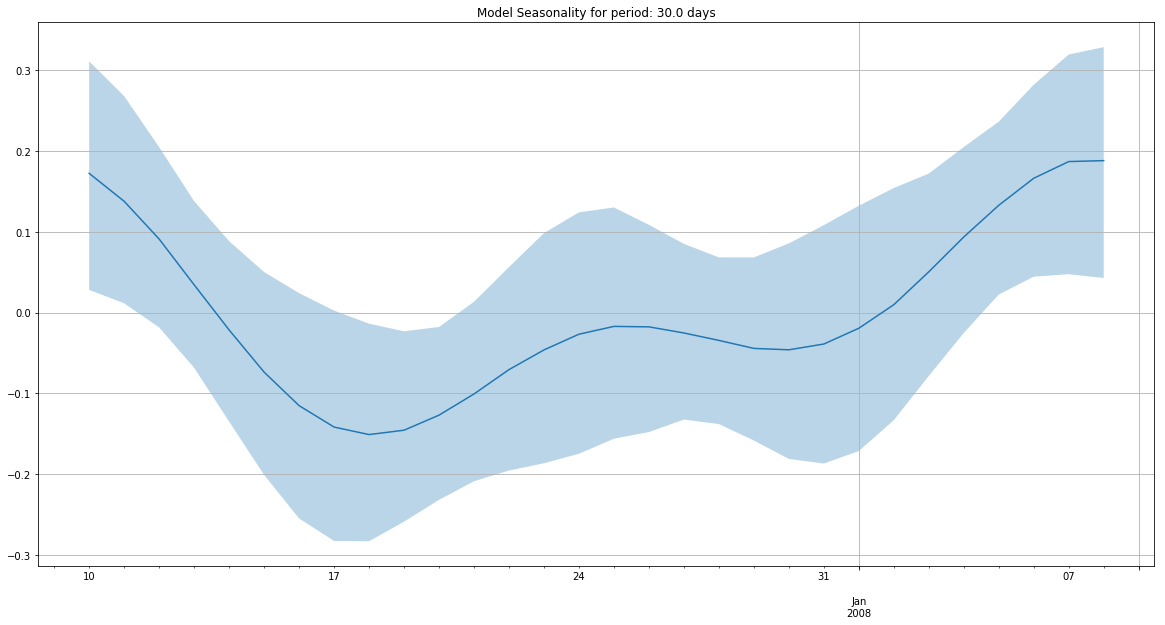
m.add_seasonality(seasonality=30, fourier_order=3)
# Add weekly seasonality (order: 3)
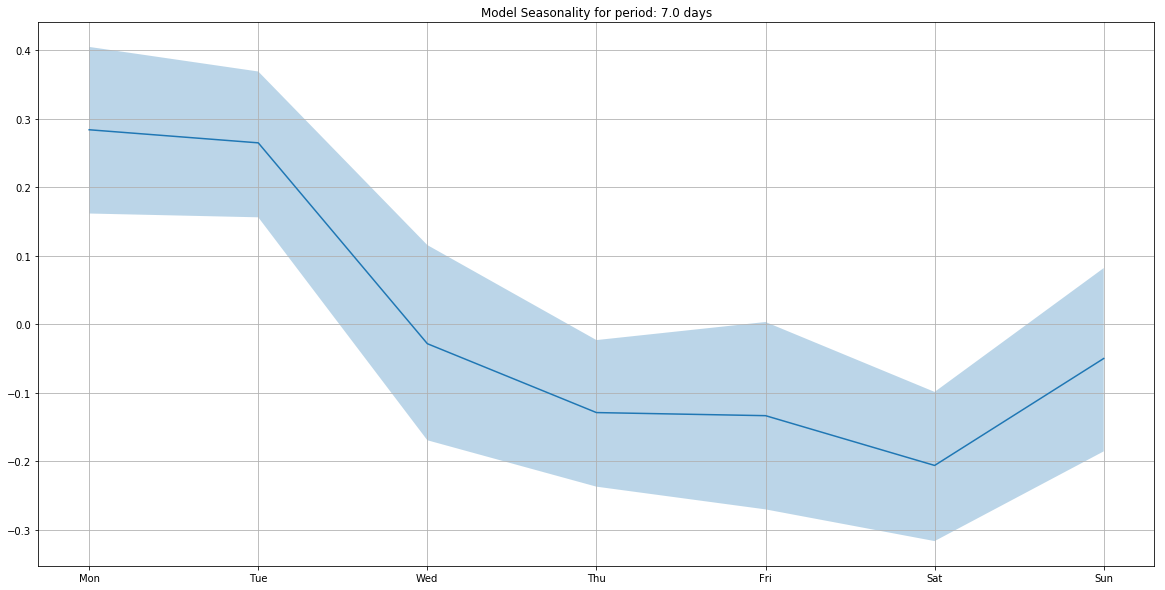
m.add_seasonality(seasonality=7, fourier_order=3)
# Fit the model (using NUTS)
m.fit(method=Sampler.NUTS)
ddf = m.predict(60, alpha=0.2, include_history=True, plot=True)
m.plot_components(
intercept=False,
)
Custom Priors
One of the main reason why PMProphet was built is to allow custom priors for the modeling.
The default priors are:
| Variable | Prior | Parameters |
|---|---|---|
regressors |
Laplace | loc:0, scale:2.5 |
holidays |
Laplace | loc:0, scale:2.5 |
seasonality |
Laplace | loc:0, scale:0.05 |
growth |
Laplace | loc:0, scale:10 |
changepoints |
Laplace | loc:0, scale:2.5 |
intercept |
Normal | loc:y.mean, scale: 2 * y.std |
sigma |
Half Cauchy | tau:10 |
But you can change model priors by inspecting and modifying the distributions stored in
m.priors
which is a dictionary of {prior: pymc3-distribution}.
In the example below we will model an additive time-series by imposing a "positive coefficients" constraint by using an Exponential distribution instead of a Laplacian distribution for the regressors.
import pandas as pd
import numpy as np
import pymc3 as pm
from pmprophet.model import PMProphet, Sampler
n_timesteps = 100
n_regressors = 20
regressors = np.random.normal(size=(n_timesteps, n_regressors))
coeffs = np.random.exponential(size=n_regressors) + np.random.normal(size=n_regressors)
# Note that min(coeffs) could be negative due to the white noise
regressors_names = [str(i) for i in range(n_regressors)]
df = pd.DataFrame()
df['y'] = np.dot(regressors, coeffs)
df['ds'] = pd.date_range('2017-01-01', periods=n_timesteps)
for idx, regressor in enumerate(regressors_names):
df[regressor] = regressors[:, idx]
m = PMProphet(df, growth=False, intercept=False, n_changepoints=0, name='model')
with m.model:
# Remember to suffix _<model-name> to the custom priors
m.priors['regressors'] = pm.Exponential('regressors_%s' % m.name, 1, shape=n_regressors)
for regressor in regressors_names:
m.add_regressor(regressor)
m.fit(
draws=10 ** 4,
method=Sampler.NUTS,
)
m.plot_components()
Automatic changepoint detection (
⚠️
experimental)
Pm-prophet is equipped with a non-parametric truncated Dirichlet Process allowing it to automatically detect changepoints in the trend.
To enable it simply initialize the model with auto_changepoints=True as follows:
from pmprophet.model import PMProphet, Sampler
import pandas as pd
df = pd.read_csv("examples/example_wp_log_peyton_manning.csv")
df = df.head(180)
m = PMProphet(df, auto_changepoints=True, growth=True, intercept=True, name='model')
m.fit(method=Sampler.METROPOLIS, draws=2000)
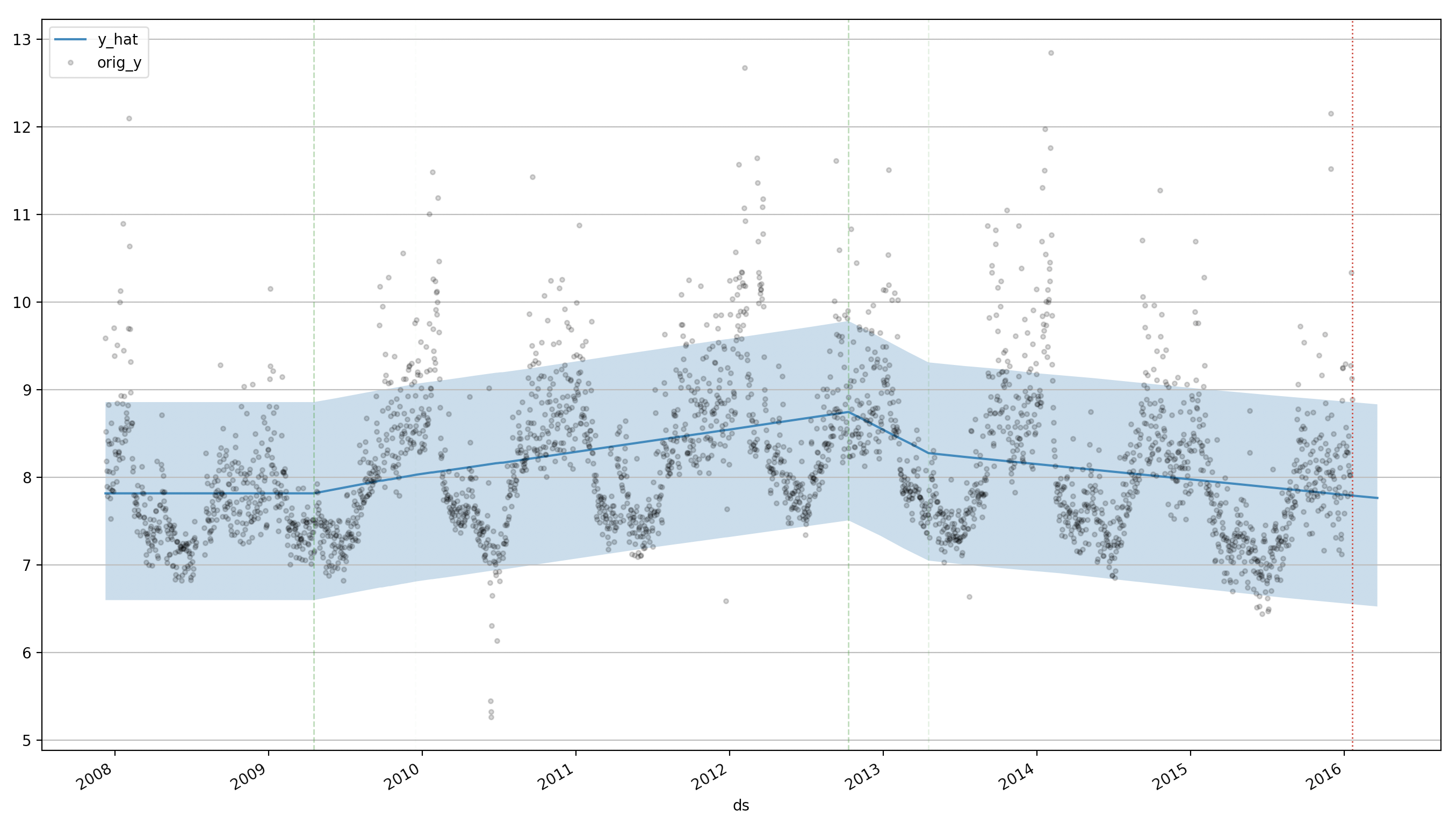
m.predict(60, alpha=0.2, include_history=True, plot=True)
m.plot_components(
intercept=False,
)
Where n_changepoints is interpreted as the truncation point for the Dirichlet Process.
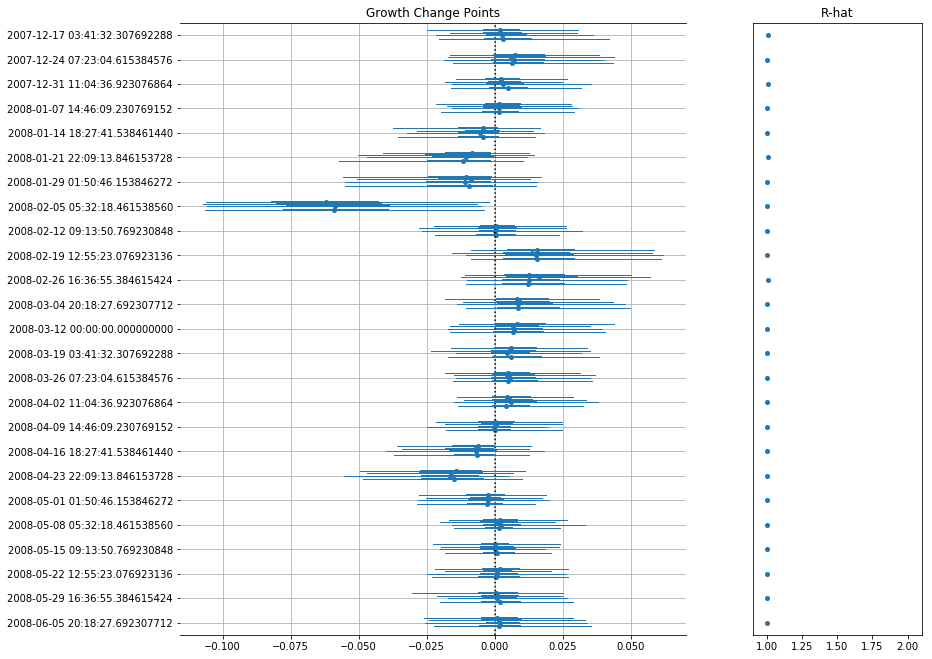
Pm-prophet will then decide which changepoint values make sense and add a custom weight to them. A call to plot_components() will reveal the changepoint map:
A few caveats exist:
- It's slow to fit since it's a non-parametric model
- For best results use NUTS as method
- It will likely require more than the default number of draws to converge
![[Feature Request] Simplify API for regressors](https://avatars.githubusercontent.com/u/2353212?v=4)
519 Jan 3, 2023
3 Feb 15, 2022
7 Dec 18, 2021
1 Dec 22, 2021
0 Jan 31, 2022
4k Jan 9, 2023
3.7k Jan 7, 2023
148 Jul 5, 2021
1.3k Dec 22, 2022
1 Nov 3, 2021
6 Dec 27, 2022
3.3k Jan 3, 2023
438 Dec 17, 2022
1.4k Dec 28, 2022
254 Dec 31, 2022
57 Dec 21, 2022
644 Dec 20, 2022
1.1k Jan 1, 2023
888 Dec 30, 2022