torch-imle
Concise and self-contained PyTorch library implementing the I-MLE gradient estimator proposed in our NeurIPS 2021 paper Implicit MLE: Backpropagating Through Discrete Exponential Family Distributions.
This repository contains a library for transforming any combinatorial black-box solver in a differentiable layer. All code for reproducing the experiments in the NeurIPS paper is available in the official NEC Laboratories Europe repository.
Overview
Implicit MLE (I-MLE) makes it possible to include discrete combinatorial optimization algorithms, such as Dijkstra's algorithm or integer linear program (ILP) solvers, in standard deep learning architectures. The core idea of I-MLE is that it defines an implicit maximum likelihood objective whose gradients are used to update upstream parameters of the model. Every instance of I-MLE requires two ingredients:
- A method to approximately sample from a complex and intractable distribution. For this we use Perturb-and-MAP (aka the Gumbel-max trick) and propose a novel family of noise perturbations tailored to the problem at hand.
- A method to compute a surrogate empirical distribution: Vanilla MLE reduces the KL divergence between the current distribution and the empirical distribution. Since in our setting, we do not have access to an empirical distribution, we have to design surrogate empirical distributions. Here we propose two families of surrogate distributions which are widely applicable and work well in practice.
Example
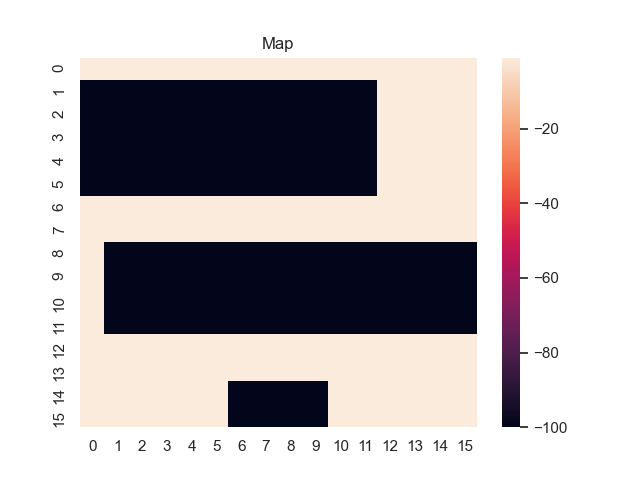
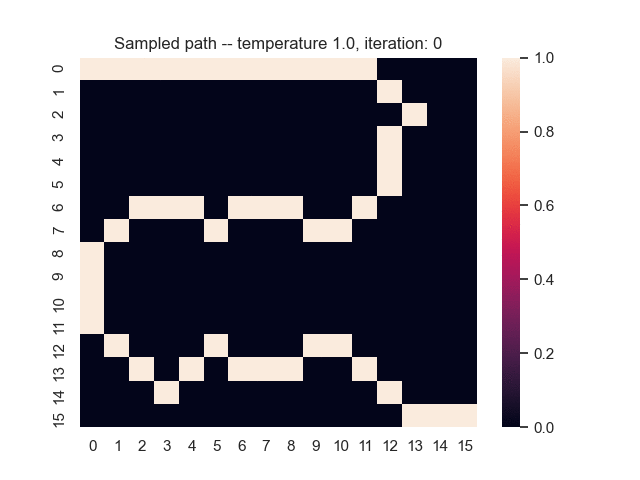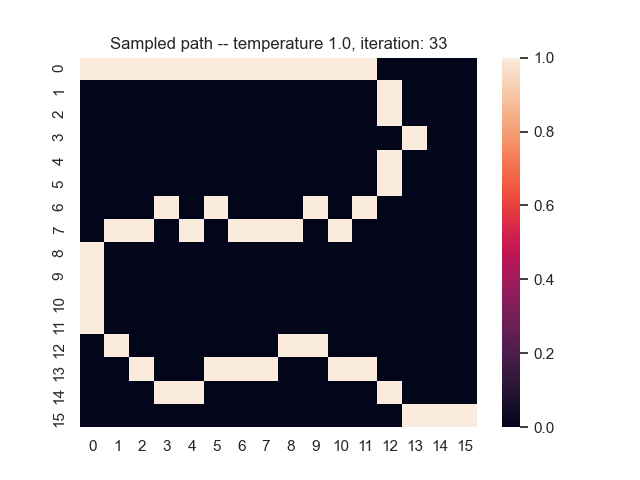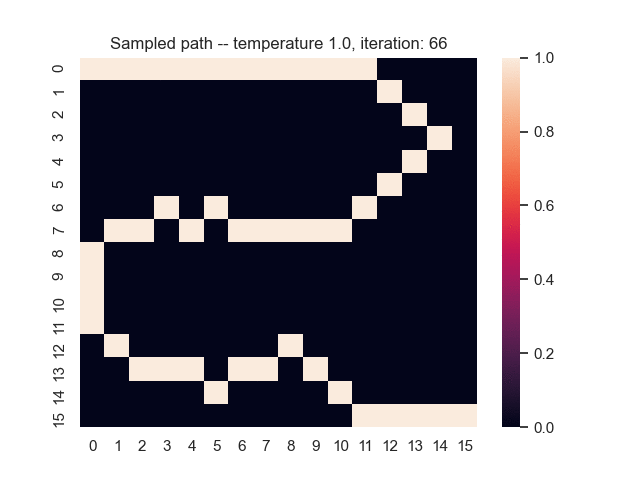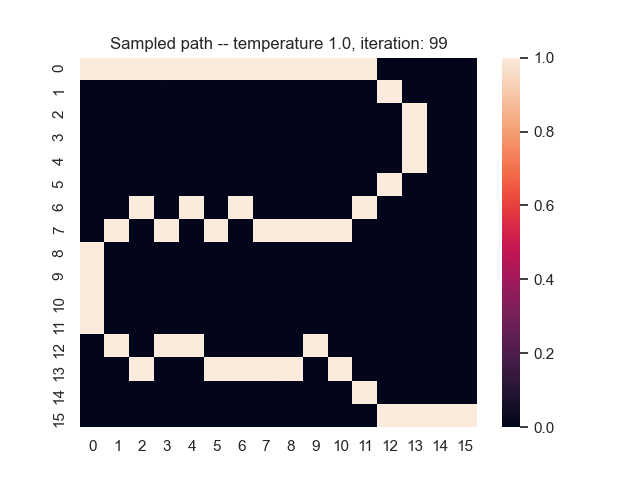
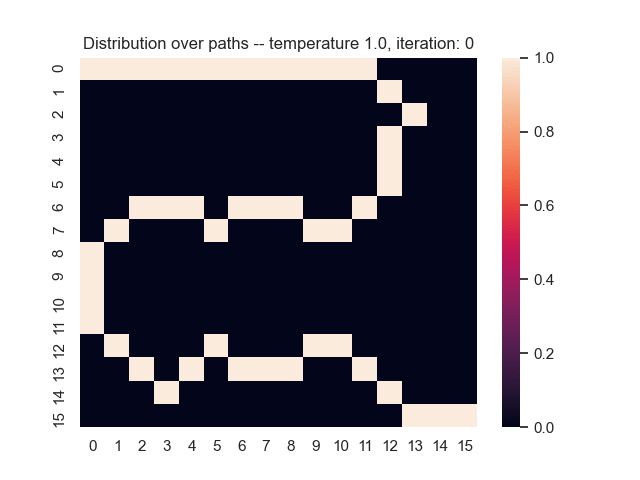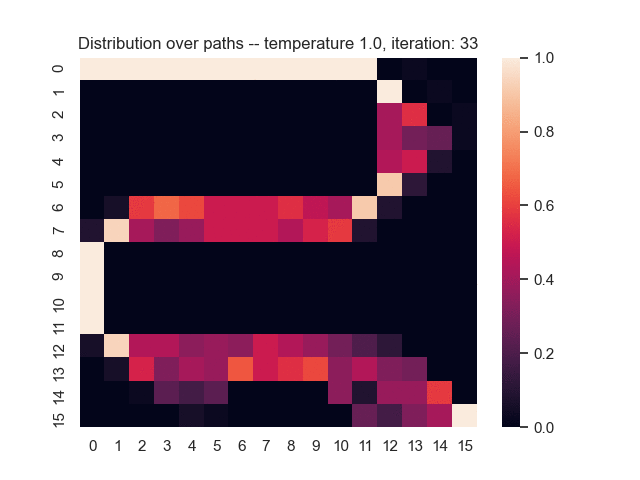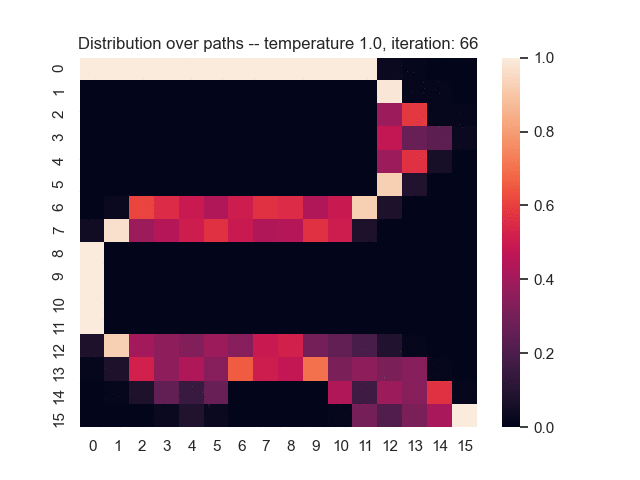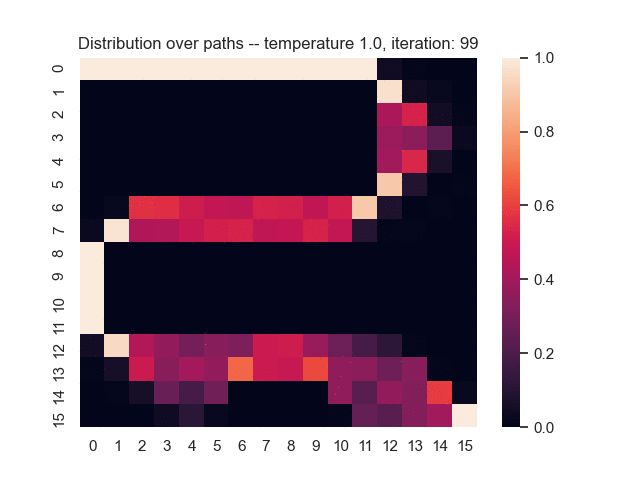
For example, let's consider a map from a simple game where the task is to find the shortest path from the top-left to the bottom-right corner. Black areas have the highest and white areas the lowest cost. In the centre, you can see what happens when we use the proposed sum-of-gamma noise distribution to sample paths. On the right, you can see the resulting marginal probabilities for every tile (the probability of each tile being part of a sampled path).
Gradients and Learning
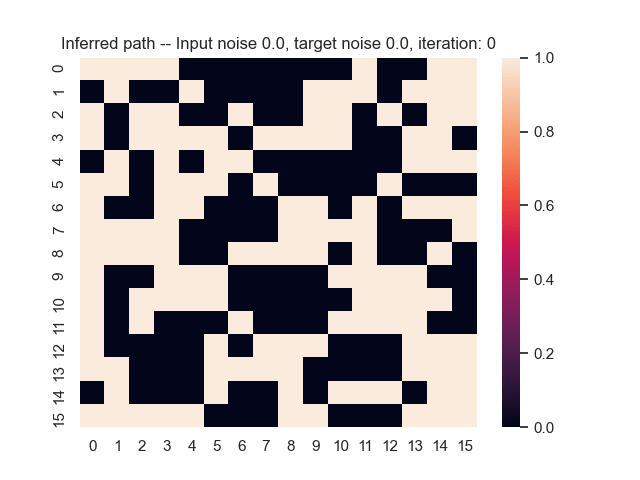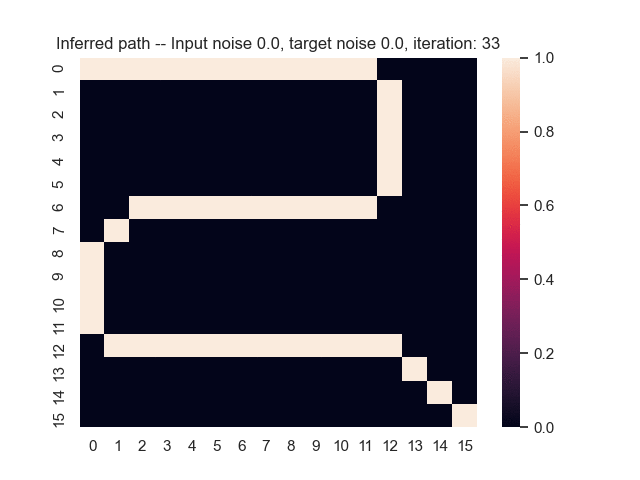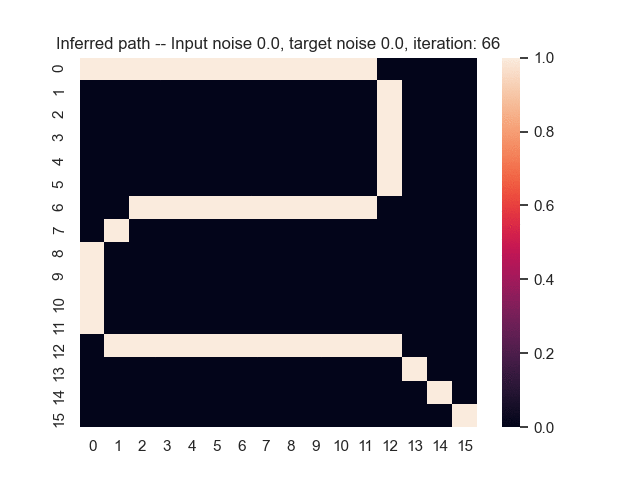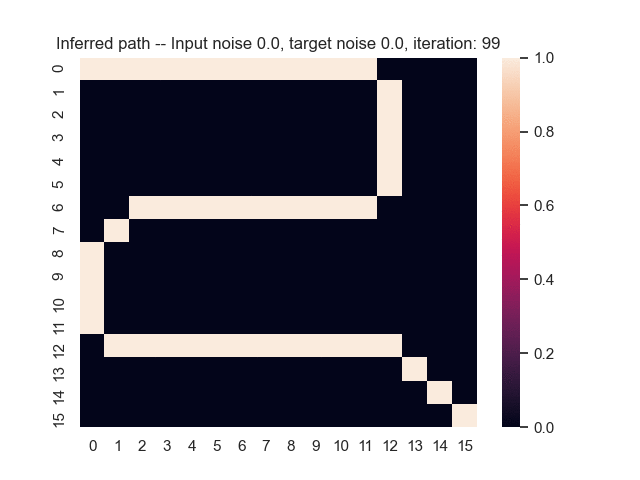
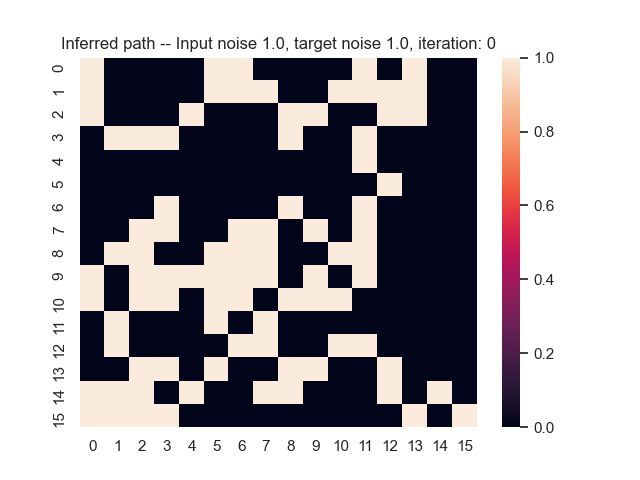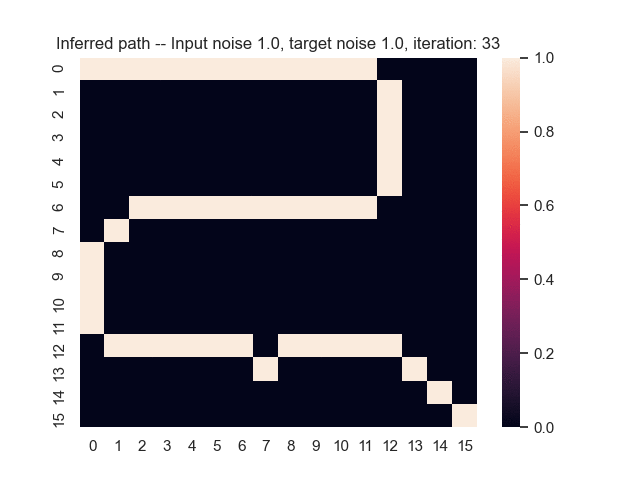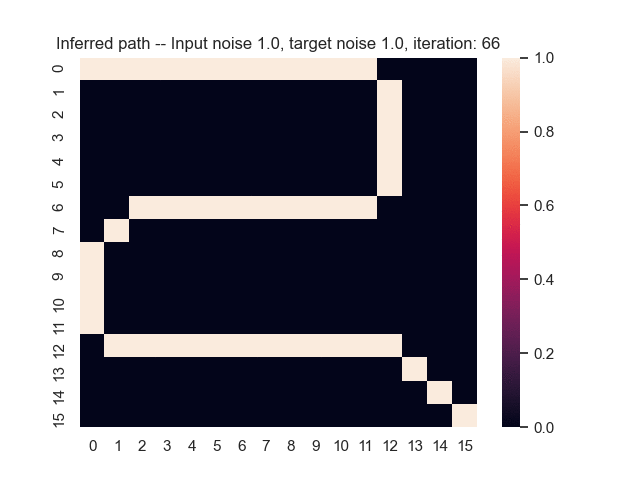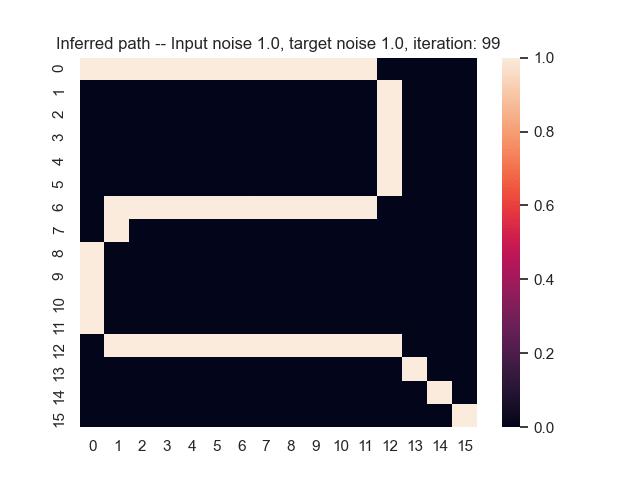
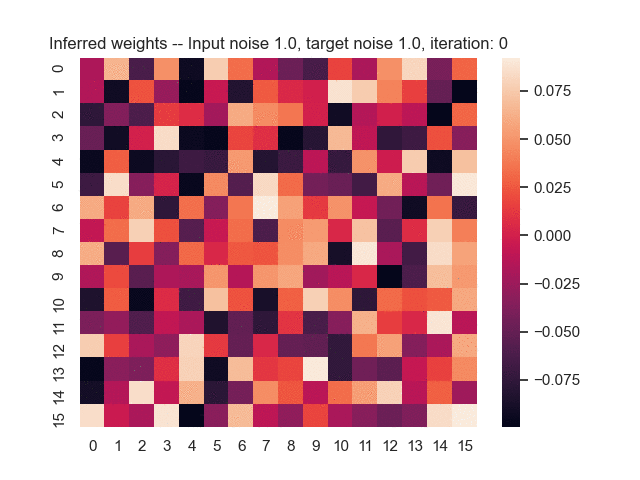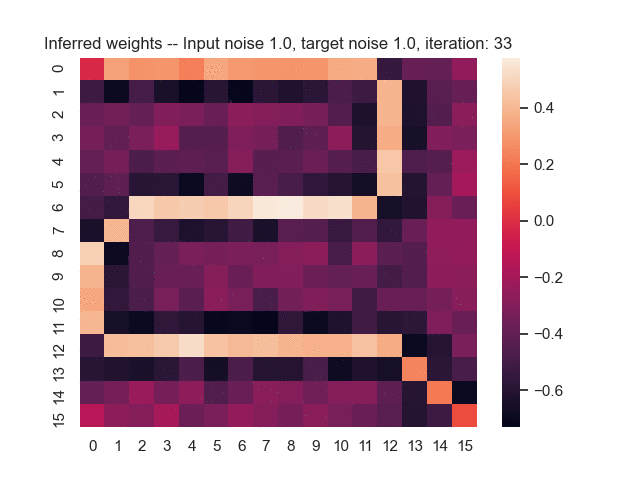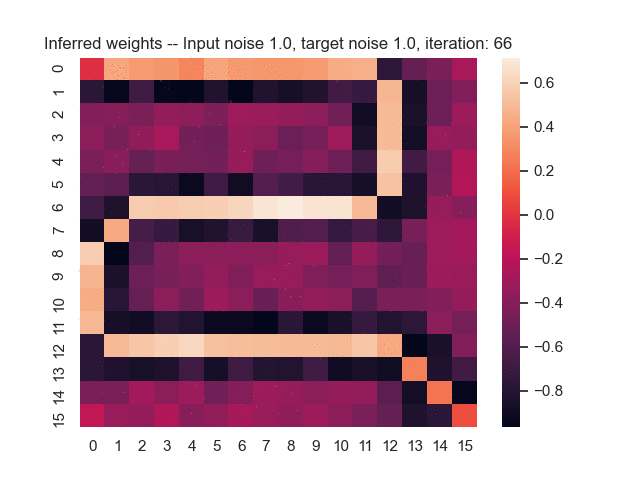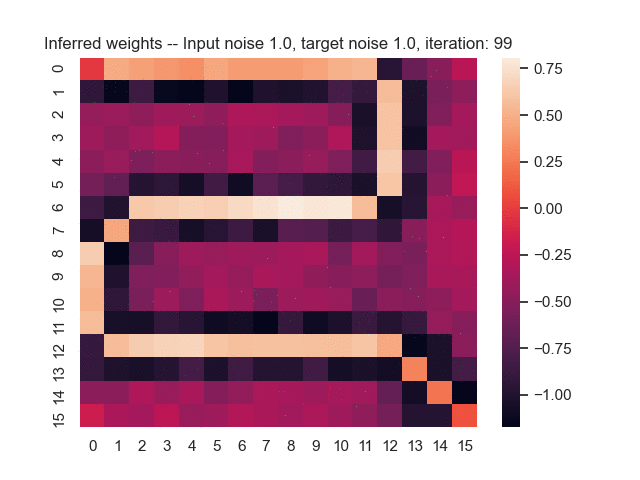
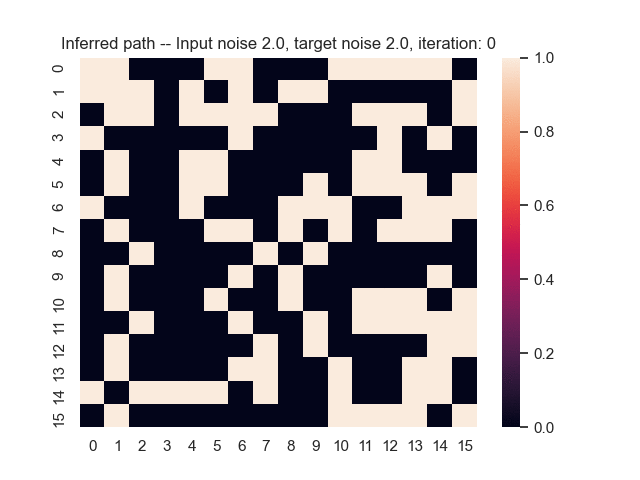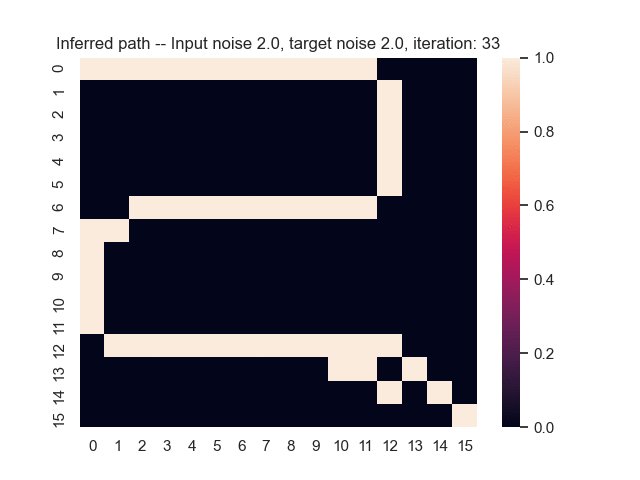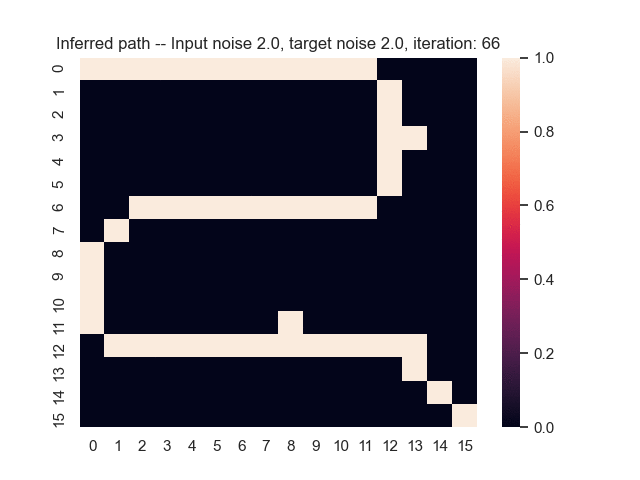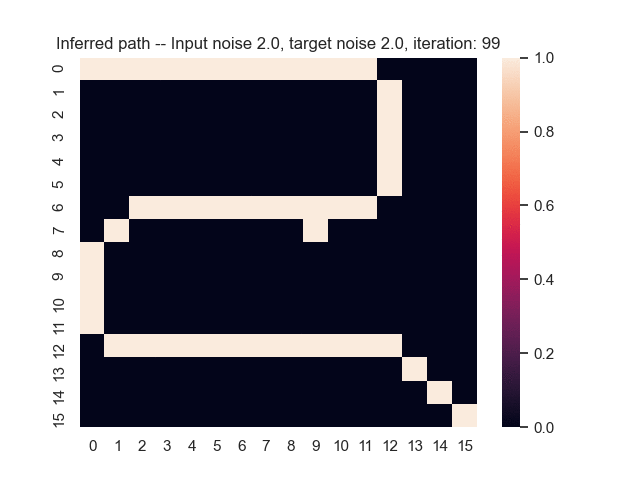
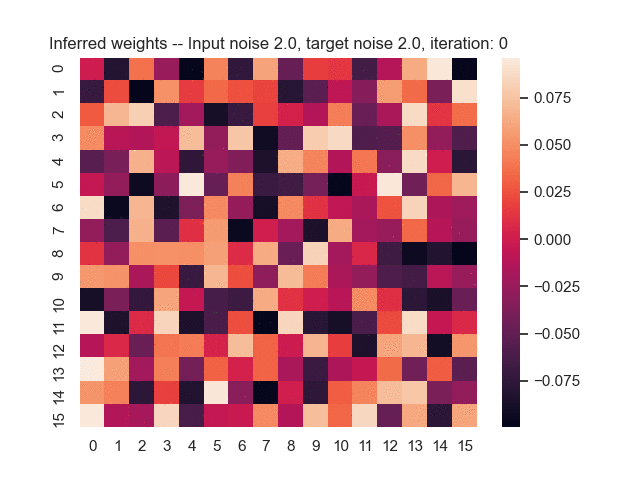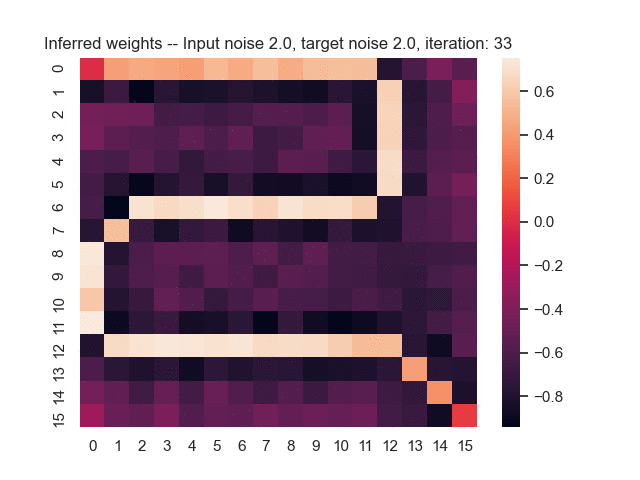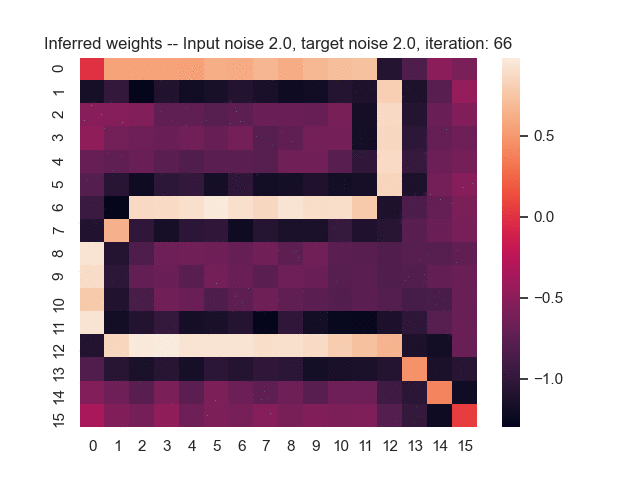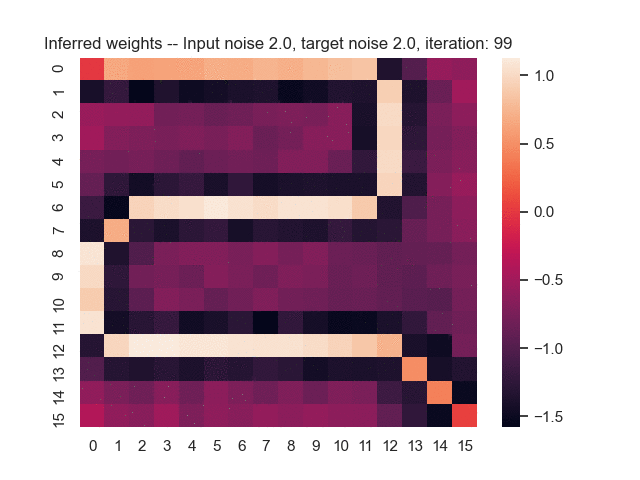
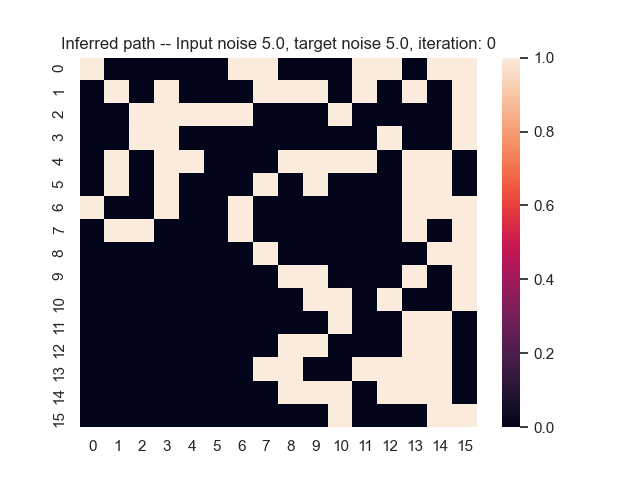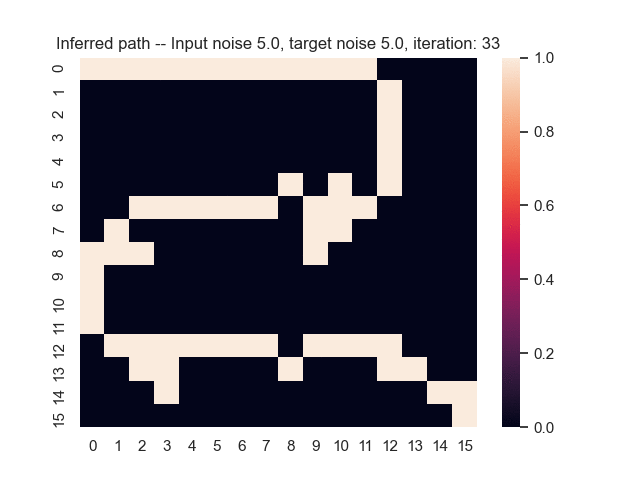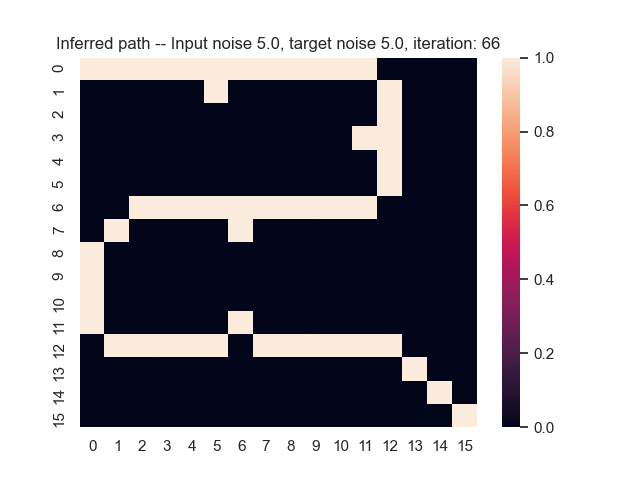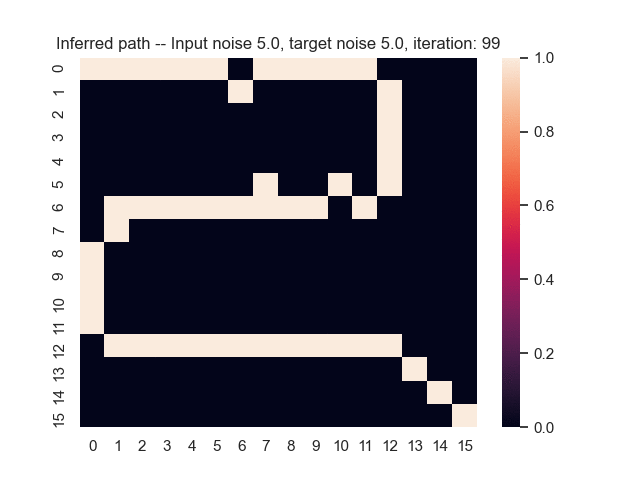
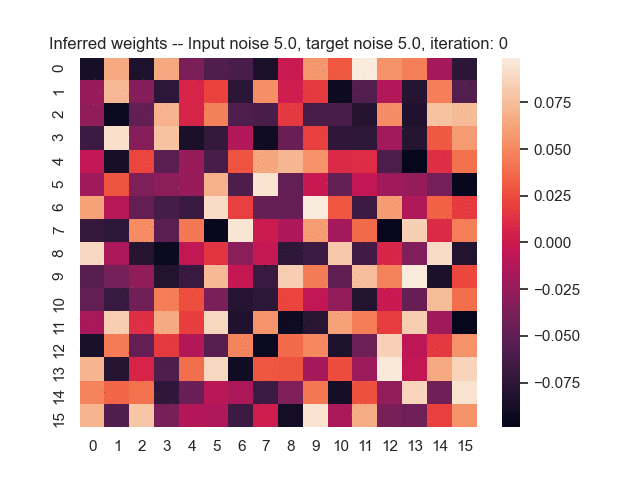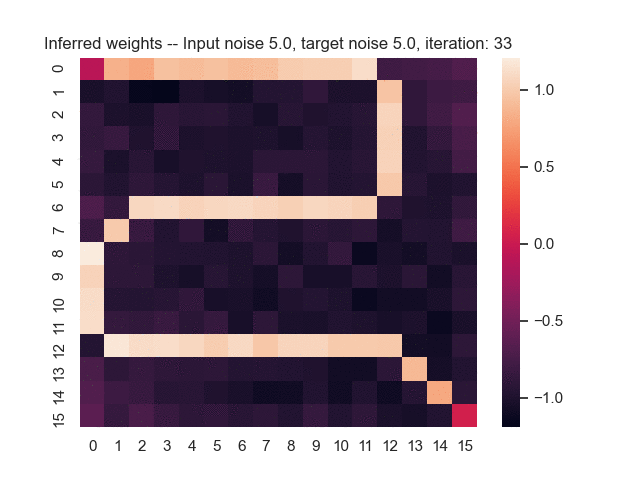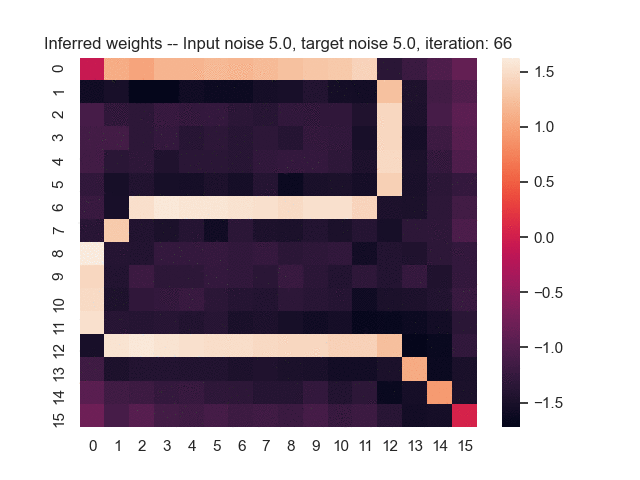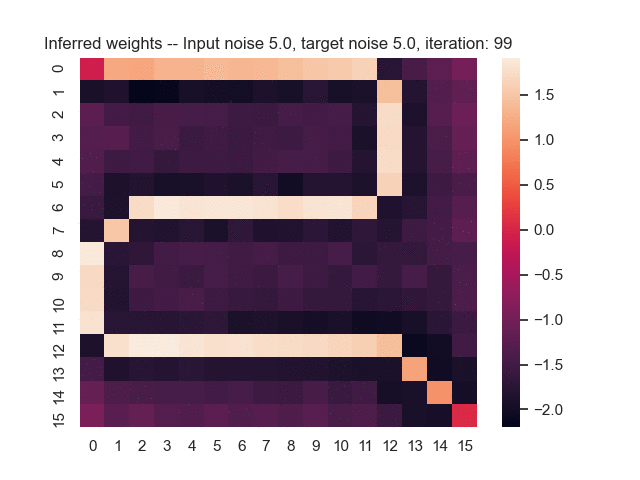
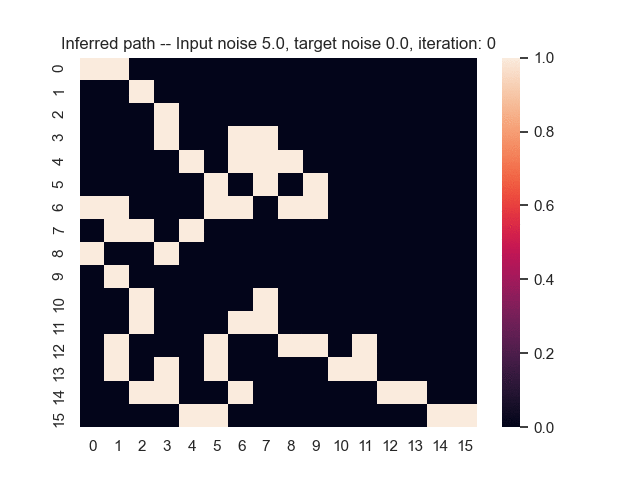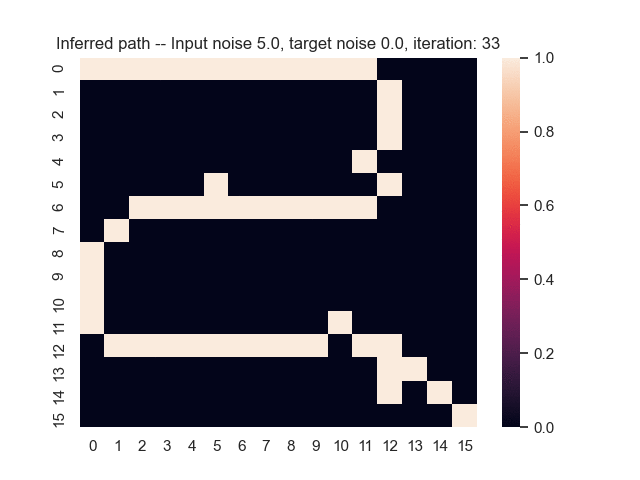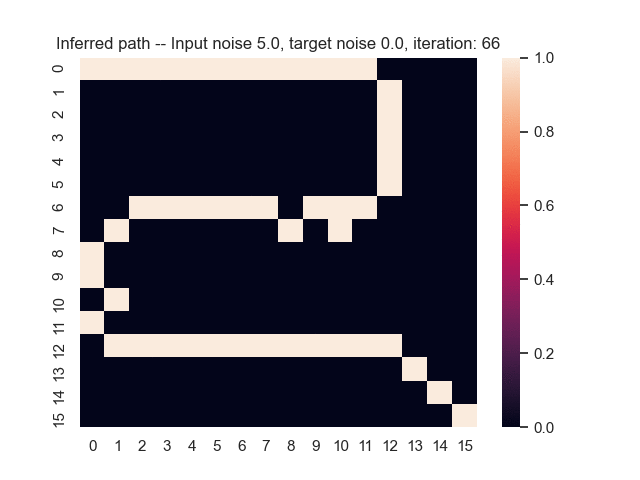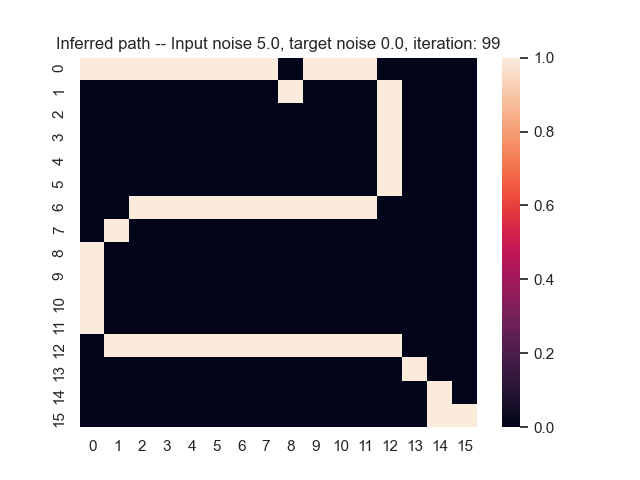
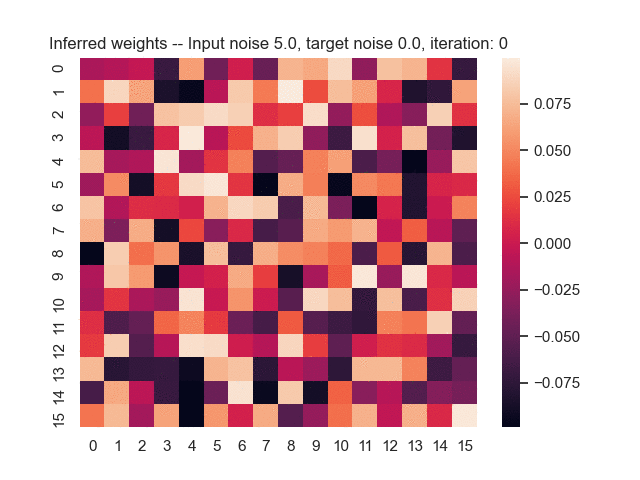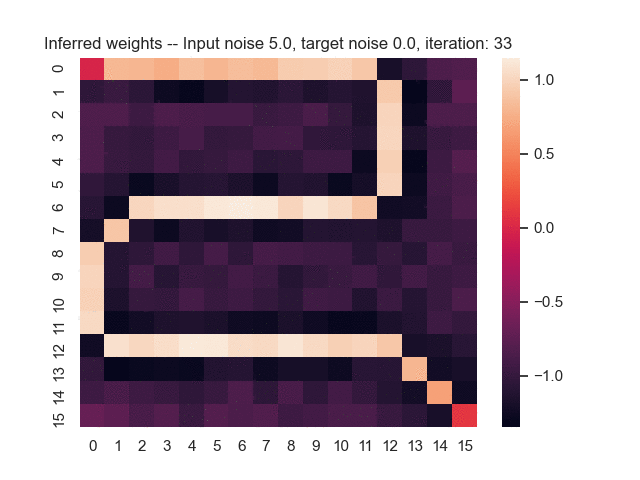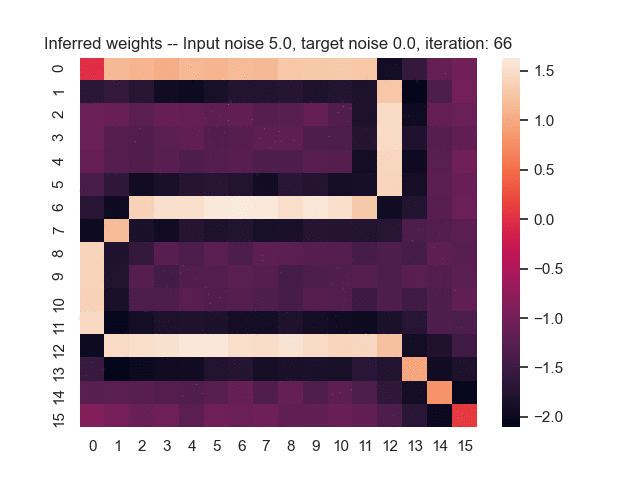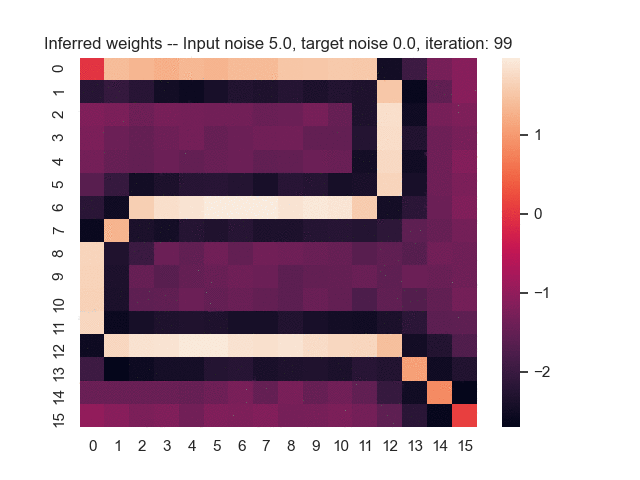
Let us assume that the optimal shortest path is the one of the left. Starting from random weights, the model can learn to produce the weights that will result in the optimal shortest path via Gradient Descent, by minimising the Hamming loss between the produced path and the gold path. Here we show the paths being produced during training (middle), and the corresponding map weights (right).
Input noise temperature set to 0.0, and target noise temperature set to 0.0:
Input noise temperature set to 1.0, and target noise temperature set to 1.0:
Input noise temperature set to 2.0, and target noise temperature set to 2.0:
Input noise temperature set to 5.0, and target noise temperature set to 5.0:
Input noise temperature set to 5.0, and target noise temperature set to 0.0:
All animations were generated by this script.
Code
Using this library is extremely easy -- see this example as a reference. Assuming we have a method that implements a black-box combinatorial solver such as Dijkstra's algorithm:
import numpy as np
import torch
from torch import Tensor
def torch_solver(weights_batch: Tensor) -> Tensor:
weights_batch = weights_batch.detach().cpu().numpy()
y_batch = np.asarray([solver(w) for w in list(weights_batch)])
return torch.tensor(y_batch, requires_grad=False)
We can obtain the corresponding distribution and gradients in this way:
from imle.wrapper import imle
from imle.target import TargetDistribution
from imle.noise import SumOfGammaNoiseDistribution
target_distribution = TargetDistribution(alpha=0.0, beta=10.0)
noise_distribution = SumOfGammaNoiseDistribution(k=k, nb_iterations=100)
def torch_solver(weights_batch: Tensor) -> Tensor:
weights_batch = weights_batch.detach().cpu().numpy()
y_batch = np.asarray([solver(w) for w in list(weights_batch)])
return torch.tensor(y_batch, requires_grad=False)
imle_solver = imle(torch_solver,
target_distribution=target_distribution,
noise_distribution=noise_distribution,
nb_samples=10,
input_noise_temperature=input_noise_temperature,
target_noise_temperature=target_noise_temperature)
Or, alternatively, using a simple function annotation:
@imle(target_distribution=target_distribution,
noise_distribution=noise_distribution,
nb_samples=10,
input_noise_temperature=input_noise_temperature,
target_noise_temperature=target_noise_temperature)
def imle_solver(weights_batch: Tensor) -> Tensor:
return torch_solver(weights_batch)
Papers using I-MLE
- Patrick Betz, Mathias Niepert, Pasquale Minervini, and Heiner Stuckenschmidt: Backpropagating through Markov Logic Networks, NeSy’20/21 @ IJCLR: 15th International Workshop on Neural-Symbolic Learning and Reasoning
Reference
@inproceedings{niepert21imle,
author = {Mathias Niepert and
Pasquale Minervini and
Luca Franceschi},
title = {Implicit {MLE:} Backpropagating Through Discrete Exponential Family
Distributions},
booktitle = {NeurIPS},
series = {Proceedings of Machine Learning Research},
publisher = {{PMLR}},
year = {2021}
}