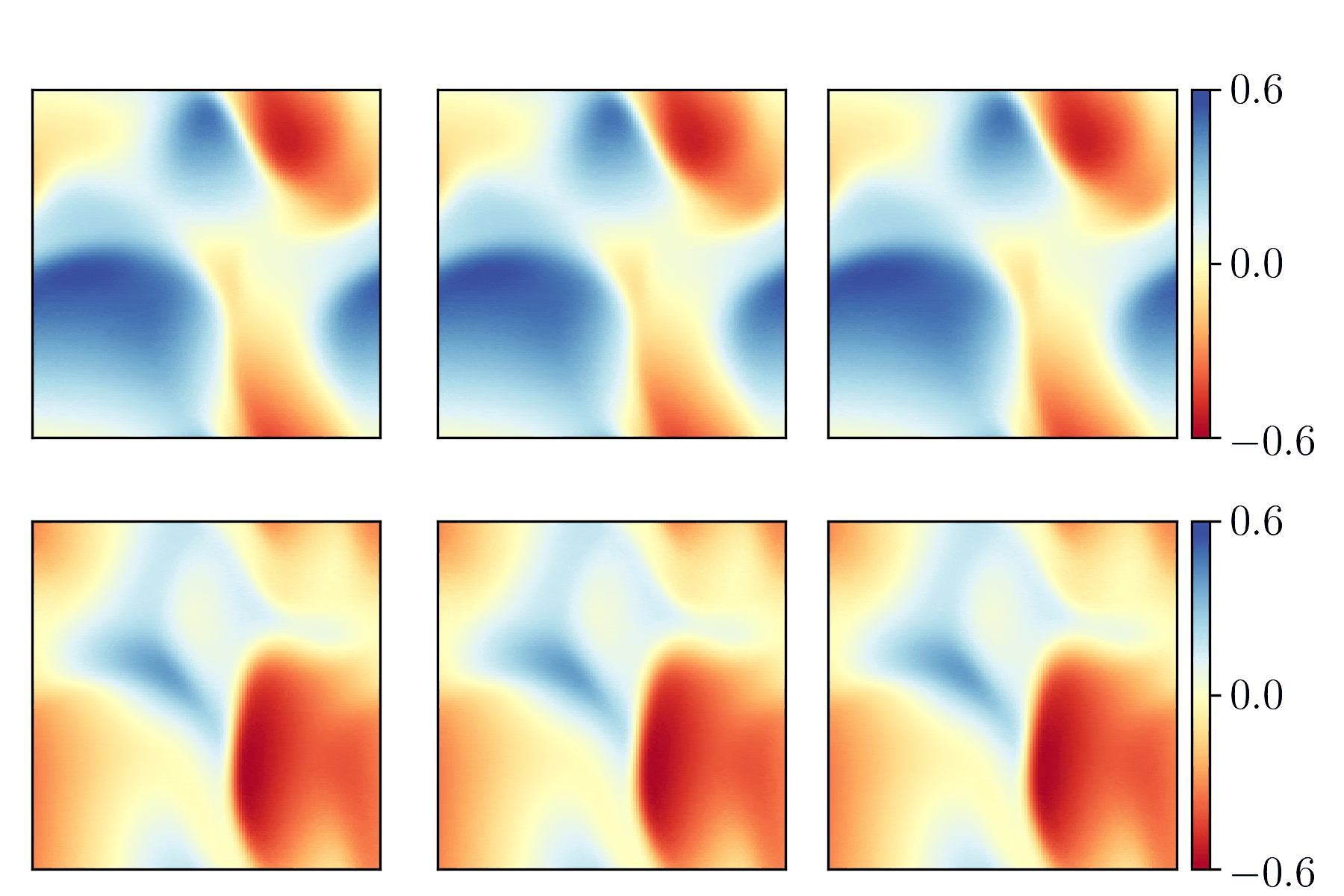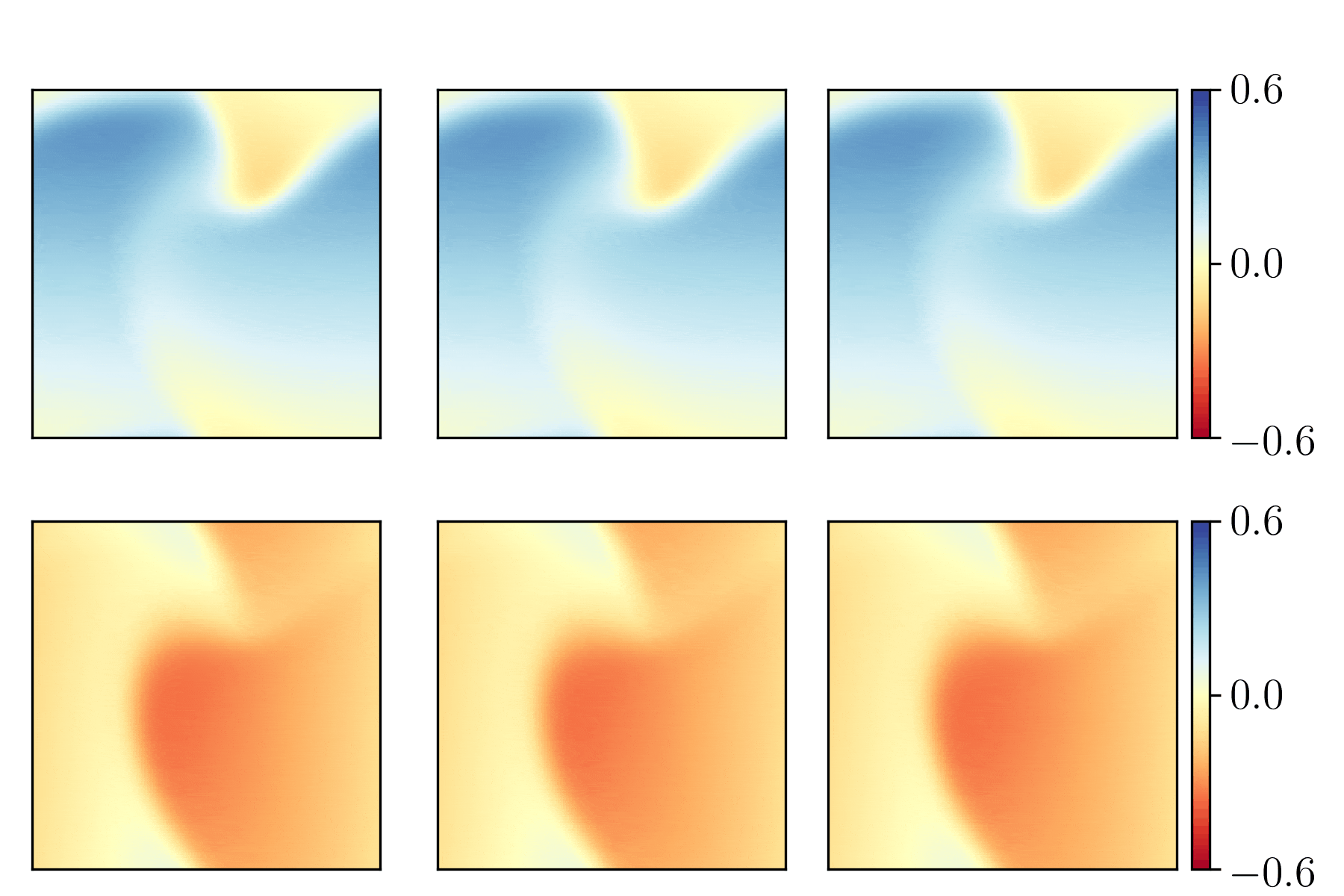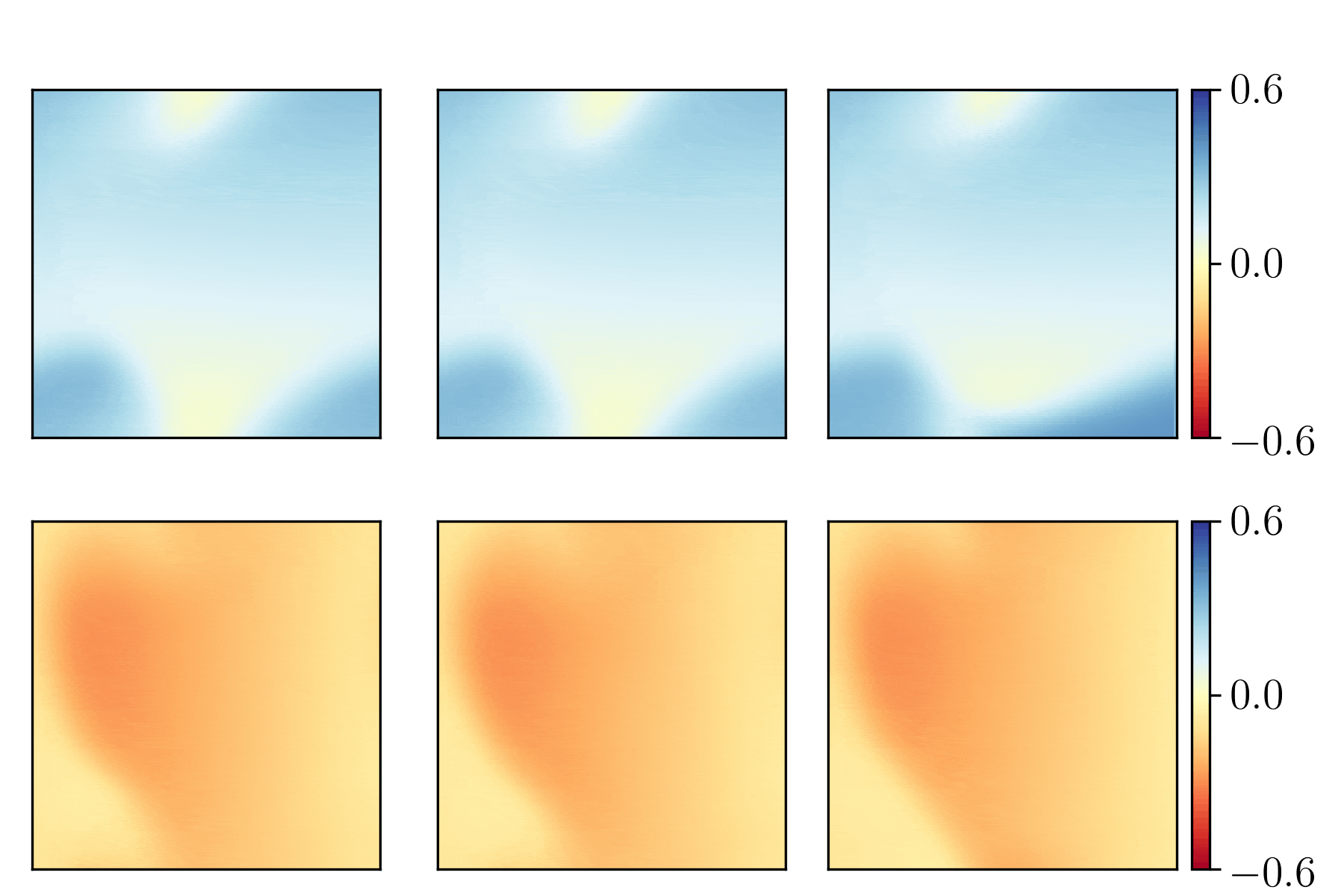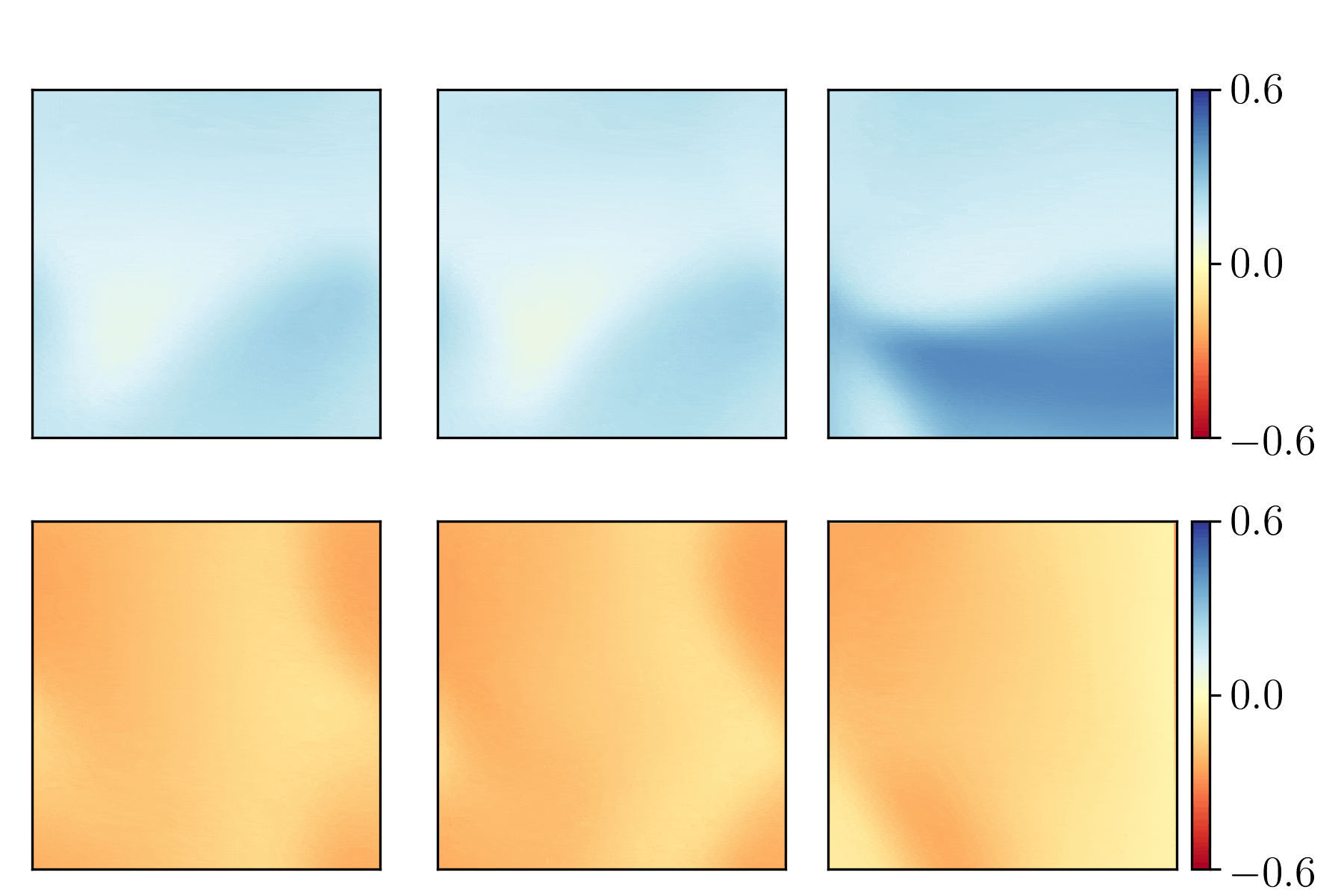
Characterizing possible failure modes in physics-informed neural networks.

Last update: Jan 2, 2023

Overview

Characterizing possible failure modes in physics-informed neural networks

This repository contains the PyTorch source code for the experiments in the manuscript:

Aditi S. Krishnapriyan, Amir Gholami, Shandian Zhe, Robert M. Kirby, Michael W. Mahoney. Characterizing possible failure modes in physics-informed neural networks., Neural Information Processing Systems (NeurIPS) 2021.

Introduction

Recent work in scientific machine learning has developed so-called physics-informed neural network (PINN) models. The typical approach is to incorporate physical domain knowledge as soft constraints on an empirical loss function and use existing machine learning methodologies to train the model. We demonstrate that, while existing PINN methodologies can learn good models for relatively trivial problems, they can easily fail to learn relevant physical phenomena even for simple PDEs. In particular, we analyze several distinct situations of widespread physical interest, including learning differential equations with convection, reaction, and diffusion operators. We provide evidence that the soft regularization in PINNs, which involves differential operators, can introduce a number of subtle problems, including making the problem ill-conditioned. Importantly, we show that these possible failure modes are not due to the lack of expressivity in the NN architecture, but that the PINN's setup makes the loss landscape very hard to optimize. We then describe two promising solutions to address these failure modes. The first approach is to use curriculum regularization, where the PINN's loss term starts from a simple PDE regularization, and becomes progressively more complex as the NN gets trained. The second approach is to pose the problem as a sequence-to-sequence learning task, rather than learning to predict the entire space-time at once. Extensive testing shows that we can achieve up to 1-2 orders of magnitude lower error with these methods as compared to regular PINN training.

Installation

Installation of all necessary packages can either be done via poetry or through requirements.txt. For example:

git clone [email protected]:a1k12/characterizing-pinns-failure-modes.git
cd characterizing-pinns-failure-modes
pip install .

Instructions

To run the code for the convection, diffusion, reaction, or reaction-diffusion ('rd') systems with periodic boundary conditions, the following can be run within the 'pbc_examples' folder.

python main_pbc.py [--system] [--seed] [--N_f] [--optimizer_name] [--lr] [--L] [--xgrid] [--nu] [--rho] [--beta] [--u0_str] [--layers] [--net] [--activation] [--loss_style] [--visualize] [--save_model]

Possible arguments:
--system            system of study (default: convection; also supports diffusion, reaction, rd)
--seed              used to reproduce the results (default: 0)
--N_f               number of points to sample from the interior domain (default: 1000)
--optimizer_name    optimizer to use, currently supports L-BFGS
--lr                learning rate (default: 1.0)
--L                 multiplier on the regularization parameter (default: 1.0)
--xgrid             size of the xgrid (default: 256)
--nu                viscosity coefficient for diffusion
--rho               reaction coefficient
--beta              speed of propagation for convection
--u0_str            initial condition (default: 'sin(x)'; also supports 'gauss' for reaction/reaction-diffusion)
--layers            number of layers in the network (default: '50,50,50,50,1')
--net               net architecture (default: 'DNN')
--activation        activation for the network (default: 'tanh')
--loss_style        loss function style (default: 'mse')
--visualize         option to visualize the solution (default: False)
--save_model        option to save the model (default: False)

Citation

This repository has been developed as part of the following paper. We would appreciate it if you would please cite the following paper if you found the library useful for your work:

@article{krishnapriyan2021characterizing,
  title={Characterizing possible failure modes in physics-informed neural networks},
  author={Krishnapriyan, Aditi S. and Gholami, Amir and Zhe, Shandian and Kirby, Robert and Mahoney, Michael W},
  journal={Advances in Neural Information Processing Systems},
  volume={34},
  year={2021}
}

Code related to "Have Your Text and Use It Too! End-to-End Neural Data-to-Text Generation with Semantic Fidelity" paper

DataTuner You have just found the DataTuner. This repository provides tools for fine-tuning language models for a task. See LICENSE.txt for license de

81 Jan 1, 2023

Handwritten Text Recognition (HTR) system implemented with TensorFlow (TF) and trained on the IAM off-line HTR dataset. This Neural Network (NN) model recognizes the text contained in the images of segmented words.

Handwritten-Text-Recognition Handwritten Text Recognition (HTR) system implemented with TensorFlow (TF) and trained on the IAM off-line HTR dataset. T

27 Jan 8, 2023

Must-read Papers on Physics-Informed Neural Networks.

PINNpapers Contributed by IDRL lab. Introduction Physics-Informed Neural Network (PINN) has achieved great success in scientific computing since 2017.

330 Jan 7, 2023

Physics-informed convolutional-recurrent neural networks for solving spatiotemporal PDEs

PhyCRNet Physics-informed convolutional-recurrent neural networks for solving spatiotemporal PDEs Paper link: [ArXiv] By: Pu Ren, Chengping Rao, Yang

11 Aug 23, 2022

A Powerful Tool For Making Combo List(All possible modes)

ComboMaker A Powerful Tool For Making Combo List Introduction Check out all possible Combo list build modes with this tool =) How to Install Open the

7 Jan 7, 2023

IDRLnet, a Python toolbox for modeling and solving problems through Physics-Informed Neural Network (PINN) systematically.

IDRLnet IDRLnet is a machine learning library on top of PyTorch. Use IDRLnet if you need a machine learning library that solves both forward and inver

105 Dec 17, 2022

PINN(s): Physics-Informed Neural Network(s) for von Karman vortex street

PINN(s): Physics-Informed Neural Network(s) for von Karman vortex street This is

2 Apr 18, 2022

A python implementation of Physics-informed Spline Learning for nonlinear dynamics discovery

PiSL A python implementation of Physics-informed Spline Learning for nonlinear dynamics discovery. Sun, F., Liu, Y. and Sun, H., 2021. Physics-informe

8 Jul 13, 2022

Spectral decomposition for characterizing long-range interaction profiles in Hi-C maps

Inspectral Spectral decomposition for characterizing long-range interaction prof

6 Dec 13, 2022

A listener for RF = 4.0 that prints a Stack Trace to console to faster find the code section where the failure appears.

robotframework-stacktrace A listener for RF = 4.0 that prints a Stack Trace to console to faster find the code section where the failure appears. Ins

16 Nov 24, 2022

pytest plugin for distributed testing and loop-on-failures testing modes.

xdist: pytest distributed testing plugin The pytest-xdist plugin extends pytest with some unique test execution modes: test run parallelization: if yo

1.1k Dec 30, 2022

Vericopy - This Python script provides various usage modes for secure local file copying and hashing.

Vericopy This Python script provides various usage modes for secure local file copying and hashing. Hash data is captured and logged for paths before

15 Nov 5, 2022

A lightweight wrapper for PyTorch that provides a simple declarative API for context switching between devices, distributed modes, mixed-precision, and PyTorch extensions.

56 Sep 13, 2022

Minesweeper clone with 3 modes of difficulty, UI scaling and custom games feature.

Insect Sweeper Minesweeper clone with 3 modes of difficulty, UI scaling and custom games feature. Mines are replaced with random insects that a player

1 Nov 5, 2021

A set of scripts for a two-step procedure to measure the value of access to destinations across several modes of travel within a geographic area.

Institute for Transportation and Development Policy

2 Oct 16, 2022

Active Transport Analytics Model (ATAM) is a new strategic transport modelling and data visualization framework for Active Transport as well as emerging micro-mobility modes

{ATAM} Active Transport Analytics Model Active Transport Analytics Model (“ATAM”) is a new strategic transport modelling and data visualization framew

0 Jan 12, 2022

Comments

Ground truth generated for the reaction diffusion equation and reaction equation

The ground truth (exact) data generated for the reaction diffusion equation with $\rho=5$ and $\nu=5$ using the code is different from that of the paper.

Here is the ground truth shown in the paper:

Here is the one I get from the code:

The same happens for the reaction equation as well. Could you please help me figure out if its the problem of the ground-truth generation or I'm doing something wrong?

Thanks, Arka

opened by arkadaw9 0

Characterizing possible failure modes in physics-informed neural networks.

Related tags

Overview

Characterizing possible failure modes in physics-informed neural networks

Introduction

Installation

Instructions

Citation

You might also like...

Code related to "Have Your Text and Use It Too! End-to-End Neural Data-to-Text Generation with Semantic Fidelity" paper

Handwritten Text Recognition (HTR) system implemented with TensorFlow (TF) and trained on the IAM off-line HTR dataset. This Neural Network (NN) model recognizes the text contained in the images of segmented words.

Must-read Papers on Physics-Informed Neural Networks.

Physics-informed convolutional-recurrent neural networks for solving spatiotemporal PDEs

A Powerful Tool For Making Combo List(All possible modes)

IDRLnet, a Python toolbox for modeling and solving problems through Physics-Informed Neural Network (PINN) systematically.

PINN(s): Physics-Informed Neural Network(s) for von Karman vortex street

A python implementation of Physics-informed Spline Learning for nonlinear dynamics discovery

Spectral decomposition for characterizing long-range interaction profiles in Hi-C maps

A listener for RF = 4.0 that prints a Stack Trace to console to faster find the code section where the failure appears.

pytest plugin for distributed testing and loop-on-failures testing modes.

Vericopy - This Python script provides various usage modes for secure local file copying and hashing.

A lightweight wrapper for PyTorch that provides a simple declarative API for context switching between devices, distributed modes, mixed-precision, and PyTorch extensions.

Minesweeper clone with 3 modes of difficulty, UI scaling and custom games feature.

A set of scripts for a two-step procedure to measure the value of access to destinations across several modes of travel within a geographic area.

Active Transport Analytics Model (ATAM) is a new strategic transport modelling and data visualization framework for Active Transport as well as emerging micro-mobility modes

OpenSea-Python-Bot - OpenSea Python Bot can be used in 2 modes

A complete python calculator with 2 modes Float and Int numbers.

Official PyTorch implementation of "Physics-aware Difference Graph Networks for Sparsely-Observed Dynamics".

Comments

Ground truth generated for the reaction diffusion equation and reaction equation

Owner

Aditi Krishnapriyan

Convolutional Recurrent Neural Networks(CRNN) for Scene Text Recognition

Code for the paper "DewarpNet: Single-Image Document Unwarping With Stacked 3D and 2D Regression Networks" (ICCV '19)

A small C++ implementation of LSTM networks, focused on OCR.

This repository contains the code for the paper "SCANimate: Weakly Supervised Learning of Skinned Clothed Avatar Networks"

Handwriting Recognition System based on a deep Convolutional Recurrent Neural Network architecture

Use Convolutional Recurrent Neural Network to recognize the Handwritten line text image without pre segmentation into words or characters. Use CTC loss Function to train.

The code of "Mask TextSpotter: An End-to-End Trainable Neural Network for Spotting Text with Arbitrary Shapes"

Code for the paper STN-OCR: A single Neural Network for Text Detection and Text Recognition

TextBoxes: A Fast Text Detector with a Single Deep Neural Network https://github.com/MhLiao/TextBoxes 基于SSD改进的文本检测算法，textBoxes_note记录了之前整理的笔记。

This is the implementation of the paper "Gated Recurrent Convolution Neural Network for OCR"