Yolo v4, v3 and v2 for Windows and Linux
(neural networks for object detection)
Paper YOLO v4: https://arxiv.org/abs/2004.10934
Paper Scaled YOLO v4: * CVPR 2021: use to reproduce results: ScaledYOLOv4
More details in articles on medium:
Manual: https://github.com/AlexeyAB/darknet/wiki
Discussion:
About Darknet framework: http://pjreddie.com/darknet/
-
Yolo v4 in other frameworks (TensorRT, TensorFlow, PyTorch, OpenVINO, OpenCV-dnn, TVM,...)
-
Yolo v4, v3 and v2 for Windows and Linux
- (neural networks for object detection)
- GeForce RTX 2080 Ti
- Requirements for Windows, Linux and macOS
- Yolo v4 in other frameworks
- Improvements in this repository
- How to compile on Linux/macOS (using
CMake) - Using also PowerShell
- How to compile on Linux (using
make) - How to compile on Windows (using
CMake) - How to compile on Windows (using
vcpkg)
- How to train with multi-GPU
- How to train (to detect your custom objects)
- When should I stop training
- How to improve object detection
- How to mark bounded boxes of objects and create annotation files
- How to use Yolo as DLL and SO libraries
- Citation
- (neural networks for object detection)
 AP50:95 - FPS (Tesla V100) Paper: https://arxiv.org/abs/2011.08036
AP50:95 - FPS (Tesla V100) Paper: https://arxiv.org/abs/2011.08036
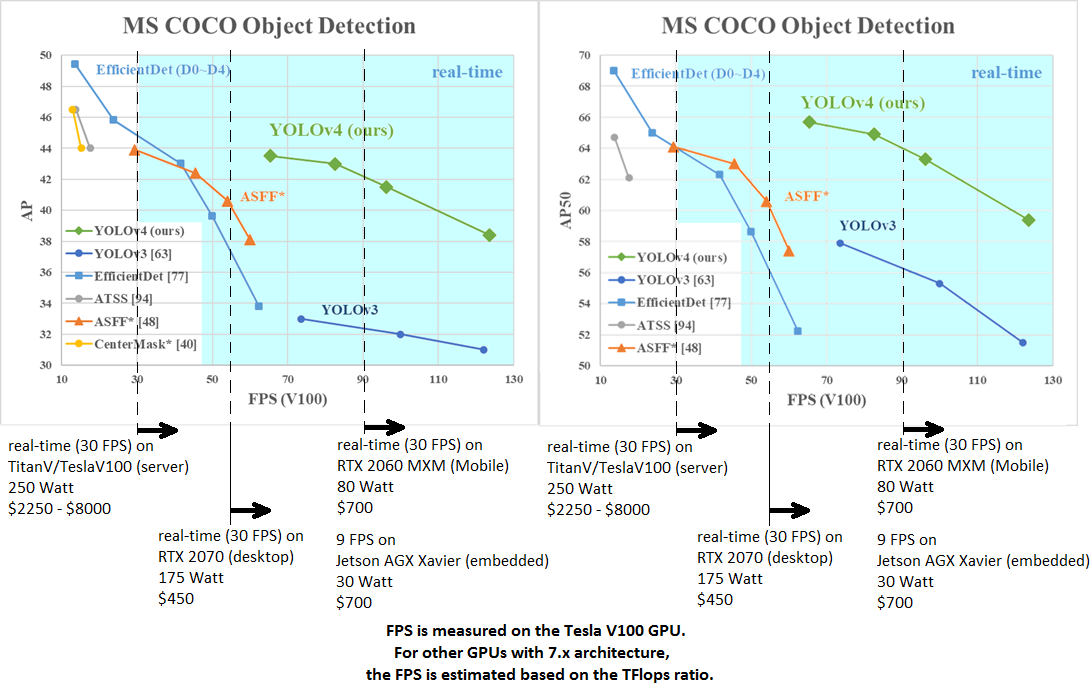 AP50:95 / AP50 - FPS (Tesla V100) Paper: https://arxiv.org/abs/2004.10934
AP50:95 / AP50 - FPS (Tesla V100) Paper: https://arxiv.org/abs/2004.10934
tkDNN-TensorRT accelerates YOLOv4 ~2x times for batch=1 and 3x-4x times for batch=4.
- tkDNN: https://github.com/ceccocats/tkDNN
- OpenCV: https://gist.github.com/YashasSamaga/48bdb167303e10f4d07b754888ddbdcf
GeForce RTX 2080 Ti
| Network Size | Darknet, FPS (avg) | tkDNN TensorRT FP32, FPS | tkDNN TensorRT FP16, FPS | OpenCV FP16, FPS | tkDNN TensorRT FP16 batch=4, FPS | OpenCV FP16 batch=4, FPS | tkDNN Speedup |
|---|---|---|---|---|---|---|---|
| 320 | 100 | 116 | 202 | 183 | 423 | 430 | 4.3x |
| 416 | 82 | 103 | 162 | 159 | 284 | 294 | 3.6x |
| 512 | 69 | 91 | 134 | 138 | 206 | 216 | 3.1x |
| 608 | 53 | 62 | 103 | 115 | 150 | 150 | 2.8x |
| Tiny 416 | 443 | 609 | 790 | 773 | 1774 | 1353 | 3.5x |
| Tiny 416 CPU Core i7 7700HQ | 3.4 | - | - | 42 | - | 39 | 12x |
- Yolo v4 Full comparison: map_fps
- Yolo v4 tiny comparison: tiny_fps
- CSPNet: paper and map_fps comparison: https://github.com/WongKinYiu/CrossStagePartialNetworks
- Yolo v3 on MS COCO: Speed / Accuracy ([email protected]) chart
- Yolo v3 on MS COCO (Yolo v3 vs RetinaNet) - Figure 3: https://arxiv.org/pdf/1804.02767v1.pdf
- Yolo v2 on Pascal VOC 2007: https://hsto.org/files/a24/21e/068/a2421e0689fb43f08584de9d44c2215f.jpg
- Yolo v2 on Pascal VOC 2012 (comp4): https://hsto.org/files/3a6/fdf/b53/3a6fdfb533f34cee9b52bdd9bb0b19d9.jpg
Youtube video of results
 |
 |
|---|
Others: https://www.youtube.com/user/pjreddie/videos
How to evaluate AP of YOLOv4 on the MS COCO evaluation server
- Download and unzip test-dev2017 dataset from MS COCO server: http://images.cocodataset.org/zips/test2017.zip
- Download list of images for Detection tasks and replace the paths with yours: https://raw.githubusercontent.com/AlexeyAB/darknet/master/scripts/testdev2017.txt
- Download
yolov4.weightsfile 245 MB: yolov4.weights (Google-drive mirror yolov4.weights ) - Content of the file
cfg/coco.datashould be
classes= 80
train = <replace with your path>/trainvalno5k.txt
valid = <replace with your path>/testdev2017.txt
names = data/coco.names
backup = backup
eval=coco
- Create
/results/folder near with./darknetexecutable file - Run validation:
./darknet detector valid cfg/coco.data cfg/yolov4.cfg yolov4.weights - Rename the file
/results/coco_results.jsontodetections_test-dev2017_yolov4_results.jsonand compress it todetections_test-dev2017_yolov4_results.zip - Submit file
detections_test-dev2017_yolov4_results.zipto the MS COCO evaluation server for thetest-dev2019 (bbox)
How to evaluate FPS of YOLOv4 on GPU
- Compile Darknet with
GPU=1 CUDNN=1 CUDNN_HALF=1 OPENCV=1in theMakefile - Download
yolov4.weightsfile 245 MB: yolov4.weights (Google-drive mirror yolov4.weights ) - Get any .avi/.mp4 video file (preferably not more than 1920x1080 to avoid bottlenecks in CPU performance)
- Run one of two commands and look at the AVG FPS:
- include video_capturing + NMS + drawing_bboxes:
./darknet detector demo cfg/coco.data cfg/yolov4.cfg yolov4.weights test.mp4 -dont_show -ext_output - exclude video_capturing + NMS + drawing_bboxes:
./darknet detector demo cfg/coco.data cfg/yolov4.cfg yolov4.weights test.mp4 -benchmark
Pre-trained models
There are weights-file for different cfg-files (trained for MS COCO dataset):
FPS on RTX 2070 (R) and Tesla V100 (V):
-
yolov4-p6.cfg - 1280x1280 - 72.1% [email protected] (54.0% [email protected]:0.95) - 32(V) FPS - xxx BFlops (xxx FMA) - 487 MB: yolov4-p6.weights
- pre-trained weights for training: https://github.com/AlexeyAB/darknet/releases/download/darknet_yolo_v4_pre/yolov4-p6.conv.289
-
yolov4-p5.cfg - 896x896 - 70.0% [email protected] (51.6% [email protected]:0.95) - 43(V) FPS - xxx BFlops (xxx FMA) - 271 MB: yolov4-p5.weights
- pre-trained weights for training: https://github.com/AlexeyAB/darknet/releases/download/darknet_yolo_v4_pre/yolov4-p5.conv.232
-
yolov4-csp-x-swish.cfg - 640x640 - 69.9% [email protected] (51.5% [email protected]:0.95) - 23(R) FPS / 50(V) FPS - 221 BFlops (110 FMA) - 381 MB: yolov4-csp-x-swish.weights
- pre-trained weights for training: https://github.com/AlexeyAB/darknet/releases/download/darknet_yolo_v4_pre/yolov4-csp-x-swish.conv.192
-
yolov4-csp-swish.cfg - 640x640 - 68.7% [email protected] (50.0% [email protected]:0.95) - 70(V) FPS - 120 (60 FMA) - 202 MB: yolov4-csp-swish.weights
- pre-trained weights for training: https://github.com/AlexeyAB/darknet/releases/download/darknet_yolo_v4_pre/yolov4-csp-swish.conv.164
-
yolov4x-mish.cfg - 640x640 - 68.5% [email protected] (50.1% [email protected]:0.95) - 23(R) FPS / 50(V) FPS - 221 BFlops (110 FMA) - 381 MB: yolov4x-mish.weights
- pre-trained weights for training: https://github.com/AlexeyAB/darknet/releases/download/darknet_yolo_v4_pre/yolov4x-mish.conv.166
-
yolov4-csp.cfg - 202 MB: yolov4-csp.weights paper Scaled Yolo v4
just change
width=andheight=parameters inyolov4-csp.cfgfile and use the sameyolov4-csp.weightsfile for all cases:width=640 height=640in cfg: 67.4% [email protected] (48.7% [email protected]:0.95) - 70(V) FPS - 120 (60 FMA) BFlopswidth=512 height=512in cfg: 64.8% [email protected] (46.2% [email protected]:0.95) - 93(V) FPS - 77 (39 FMA) BFlops- pre-trained weights for training: https://github.com/AlexeyAB/darknet/releases/download/darknet_yolo_v4_pre/yolov4-csp.conv.142
-
yolov4.cfg - 245 MB: yolov4.weights (Google-drive mirror yolov4.weights ) paper Yolo v4 just change
width=andheight=parameters inyolov4.cfgfile and use the sameyolov4.weightsfile for all cases:width=608 height=608in cfg: 65.7% [email protected] (43.5% [email protected]:0.95) - 34(R) FPS / 62(V) FPS - 128.5 BFlopswidth=512 height=512in cfg: 64.9% [email protected] (43.0% [email protected]:0.95) - 45(R) FPS / 83(V) FPS - 91.1 BFlopswidth=416 height=416in cfg: 62.8% [email protected] (41.2% [email protected]:0.95) - 55(R) FPS / 96(V) FPS - 60.1 BFlopswidth=320 height=320in cfg: 60% [email protected] ( 38% [email protected]:0.95) - 63(R) FPS / 123(V) FPS - 35.5 BFlops
-
yolov4-tiny.cfg - 40.2% [email protected] - 371(1080Ti) FPS / 330(RTX2070) FPS - 6.9 BFlops - 23.1 MB: yolov4-tiny.weights
-
enet-coco.cfg (EfficientNetB0-Yolov3) - 45.5% [email protected] - 55(R) FPS - 3.7 BFlops - 18.3 MB: enetb0-coco_final.weights
-
yolov3-openimages.cfg - 247 MB - 18(R) FPS - OpenImages dataset: yolov3-openimages.weights
CLICK ME - Yolo v3 models
-
csresnext50-panet-spp-original-optimal.cfg - 65.4% [email protected] (43.2% [email protected]:0.95) - 32(R) FPS - 100.5 BFlops - 217 MB: csresnext50-panet-spp-original-optimal_final.weights
-
yolov3-spp.cfg - 60.6% [email protected] - 38(R) FPS - 141.5 BFlops - 240 MB: yolov3-spp.weights
-
csresnext50-panet-spp.cfg - 60.0% [email protected] - 44 FPS - 71.3 BFlops - 217 MB: csresnext50-panet-spp_final.weights
-
yolov3.cfg - 55.3% [email protected] - 66(R) FPS - 65.9 BFlops - 236 MB: yolov3.weights
-
yolov3-tiny.cfg - 33.1% [email protected] - 345(R) FPS - 5.6 BFlops - 33.7 MB: yolov3-tiny.weights
-
yolov3-tiny-prn.cfg - 33.1% [email protected] - 370(R) FPS - 3.5 BFlops - 18.8 MB: yolov3-tiny-prn.weights
CLICK ME - Yolo v2 models
yolov2.cfg(194 MB COCO Yolo v2) - requires 4 GB GPU-RAM: https://pjreddie.com/media/files/yolov2.weightsyolo-voc.cfg(194 MB VOC Yolo v2) - requires 4 GB GPU-RAM: http://pjreddie.com/media/files/yolo-voc.weightsyolov2-tiny.cfg(43 MB COCO Yolo v2) - requires 1 GB GPU-RAM: https://pjreddie.com/media/files/yolov2-tiny.weightsyolov2-tiny-voc.cfg(60 MB VOC Yolo v2) - requires 1 GB GPU-RAM: http://pjreddie.com/media/files/yolov2-tiny-voc.weightsyolo9000.cfg(186 MB Yolo9000-model) - requires 4 GB GPU-RAM: http://pjreddie.com/media/files/yolo9000.weights
Put it near compiled: darknet.exe
You can get cfg-files by path: darknet/cfg/
Requirements for Windows, Linux and macOS
- CMake >= 3.18: https://cmake.org/download/
- Powershell (already installed on windows): https://docs.microsoft.com/en-us/powershell/scripting/install/installing-powershell
- CUDA >= 10.2: https://developer.nvidia.com/cuda-toolkit-archive (on Linux do Post-installation Actions)
- OpenCV >= 2.4: use your preferred package manager (brew, apt), build from source using vcpkg or download from OpenCV official site (on Windows set system variable
OpenCV_DIR=C:\opencv\build- where are theincludeandx64folders image) - cuDNN >= 8.0.2 https://developer.nvidia.com/rdp/cudnn-archive (on Linux follow steps described here https://docs.nvidia.com/deeplearning/sdk/cudnn-install/index.html#installlinux-tar , on Windows follow steps described here https://docs.nvidia.com/deeplearning/sdk/cudnn-install/index.html#installwindows)
- GPU with CC >= 3.0: https://en.wikipedia.org/wiki/CUDA#GPUs_supported
Yolo v4 in other frameworks
- Pytorch - Scaled-YOLOv4: https://github.com/WongKinYiu/ScaledYOLOv4
- TensorFlow:
pip install yolov4YOLOv4 on TensorFlow 2.0 / TFlite / Android: https://github.com/hunglc007/tensorflow-yolov4-tflite Official TF models: https://github.com/tensorflow/models/tree/master/official/vision/beta/projects/yolo For YOLOv4 - convertyolov4.weights/cfgfiles toyolov4.pbby using TNTWEN project, and toyolov4.tfliteTensorFlow-lite - OpenCV the fastest implementation of YOLOv4 for CPU (x86/ARM-Android), OpenCV can be compiled with OpenVINO-backend for running on (Myriad X / USB Neural Compute Stick / Arria FPGA), use
yolov4.weights/cfgwith: C++ example or Python example - Intel OpenVINO 2021.2: supports YOLOv4 (NPU Myriad X / USB Neural Compute Stick / Arria FPGA): https://devmesh.intel.com/projects/openvino-yolov4-49c756 read this manual (old manual ) (for Scaled-YOLOv4 models use https://github.com/Chen-MingChang/pytorch_YOLO_OpenVINO_demo )
- PyTorch > ONNX:
- ONNX on Jetson for YOLOv4: https://developer.nvidia.com/blog/announcing-onnx-runtime-for-jetson/ and https://github.com/ttanzhiqiang/onnx_tensorrt_project
- nVidia Transfer Learning Toolkit (TLT>=3.0) Training and Detection https://docs.nvidia.com/metropolis/TLT/tlt-user-guide/text/object_detection/yolo_v4.html
- TensorRT+tkDNN: https://github.com/ceccocats/tkDNN#fps-results
- Deepstream 5.0 / TensorRT for YOLOv4 https://github.com/NVIDIA-AI-IOT/yolov4_deepstream or https://github.com/marcoslucianops/DeepStream-Yolo read Yolo is natively supported in DeepStream 4.0 and PDF. Additionally jkjung-avt/tensorrt_demos or wang-xinyu/tensorrtx
- Triton Inference Server / TensorRT https://github.com/isarsoft/yolov4-triton-tensorrt
- DirectML https://github.com/microsoft/DirectML/tree/master/Samples/yolov4
- OpenCL (Intel, AMD, Mali GPUs for macOS & GNU/Linux) https://github.com/sowson/darknet
- HIP for Training and Detection on AMD GPU https://github.com/os-hackathon/darknet
- ROS (Robot Operating System) https://github.com/engcang/ros-yolo-sort
- Xilinx Zynq Ultrascale+ Deep Learning Processor (DPU) ZCU102/ZCU104: https://github.com/Xilinx/Vitis-In-Depth-Tutorial/tree/master/Machine_Learning/Design_Tutorials/07-yolov4-tutorial
- Amazon Neurochip / Amazon EC2 Inf1 instances 1.85 times higher throughput and 37% lower cost per image for TensorFlow based YOLOv4 model, using Keras URL
- TVM - compilation of deep learning models (Keras, MXNet, PyTorch, Tensorflow, CoreML, DarkNet) into minimum deployable modules on diverse hardware backend (CPUs, GPUs, FPGA, and specialized accelerators): https://tvm.ai/about
- Tencent/ncnn: the fastest inference of YOLOv4 on mobile phone CPU: https://github.com/Tencent/ncnn
- OpenDataCam - It detects, tracks and counts moving objects by using YOLOv4: https://github.com/opendatacam/opendatacam#-hardware-pre-requisite
- Netron - Visualizer for neural networks: https://github.com/lutzroeder/netron
Datasets
- MS COCO: use
./scripts/get_coco_dataset.shto get labeled MS COCO detection dataset - OpenImages: use
python ./scripts/get_openimages_dataset.pyfor labeling train detection dataset - Pascal VOC: use
python ./scripts/voc_label.pyfor labeling Train/Test/Val detection datasets - ILSVRC2012 (ImageNet classification): use
./scripts/get_imagenet_train.sh(alsoimagenet_label.shfor labeling valid set) - German/Belgium/Russian/LISA/MASTIF Traffic Sign Datasets for Detection - use this parsers: https://github.com/angeligareta/Datasets2Darknet#detection-task
- List of other datasets: https://github.com/AlexeyAB/darknet/tree/master/scripts#datasets
Improvements in this repository
- developed State-of-the-Art object detector YOLOv4
- added State-of-Art models: CSP, PRN, EfficientNet
- added layers: [conv_lstm], [scale_channels] SE/ASFF/BiFPN, [local_avgpool], [sam], [Gaussian_yolo], [reorg3d] (fixed [reorg]), fixed [batchnorm]
- added the ability for training recurrent models (with layers conv-lstm
[conv_lstm]/conv-rnn[crnn]) for accurate detection on video - added data augmentation:
[net] mixup=1 cutmix=1 mosaic=1 blur=1. Added activations: SWISH, MISH, NORM_CHAN, NORM_CHAN_SOFTMAX - added the ability for training with GPU-processing using CPU-RAM to increase the mini_batch_size and increase accuracy (instead of batch-norm sync)
- improved binary neural network performance 2x-4x times for Detection on CPU and GPU if you trained your own weights by using this XNOR-net model (bit-1 inference) : https://github.com/AlexeyAB/darknet/blob/master/cfg/yolov3-tiny_xnor.cfg
- improved neural network performance ~7% by fusing 2 layers into 1: Convolutional + Batch-norm
- improved performance: Detection 2x times, on GPU Volta/Turing (Tesla V100, GeForce RTX, ...) using Tensor Cores if
CUDNN_HALFdefined in theMakefileordarknet.sln - improved performance ~1.2x times on FullHD, ~2x times on 4K, for detection on the video (file/stream) using
darknet detector demo... - improved performance 3.5 X times of data augmentation for training (using OpenCV SSE/AVX functions instead of hand-written functions) - removes bottleneck for training on multi-GPU or GPU Volta
- improved performance of detection and training on Intel CPU with AVX (Yolo v3 ~85%)
- optimized memory allocation during network resizing when
random=1 - optimized GPU initialization for detection - we use batch=1 initially instead of re-init with batch=1
- added correct calculation of mAP, F1, IoU, Precision-Recall using command
darknet detector map... - added drawing of chart of average-Loss and accuracy-mAP (
-mapflag) during training - run
./darknet detector demo ... -json_port 8070 -mjpeg_port 8090as JSON and MJPEG server to get results online over the network by using your soft or Web-browser - added calculation of anchors for training
- added example of Detection and Tracking objects: https://github.com/AlexeyAB/darknet/blob/master/src/yolo_console_dll.cpp
- run-time tips and warnings if you use incorrect cfg-file or dataset
- added support for Windows
- many other fixes of code...
And added manual - How to train Yolo v4-v2 (to detect your custom objects)
Also, you might be interested in using a simplified repository where is implemented INT8-quantization (+30% speedup and -1% mAP reduced): https://github.com/AlexeyAB/yolo2_light
How to use on the command line
If you use build.ps1 script or the makefile (Linux only) you will find darknet in the root directory.
If you use the deprecated Visual Studio solutions, you will find darknet in the directory \build\darknet\x64.
If you customize build with CMake GUI, darknet executable will be installed in your preferred folder.
- Yolo v4 COCO - image:
./darknet detector test cfg/coco.data cfg/yolov4.cfg yolov4.weights -thresh 0.25 - Output coordinates of objects:
./darknet detector test cfg/coco.data yolov4.cfg yolov4.weights -ext_output dog.jpg - Yolo v4 COCO - video:
./darknet detector demo cfg/coco.data cfg/yolov4.cfg yolov4.weights -ext_output test.mp4 - Yolo v4 COCO - WebCam 0:
./darknet detector demo cfg/coco.data cfg/yolov4.cfg yolov4.weights -c 0 - Yolo v4 COCO for net-videocam - Smart WebCam:
./darknet detector demo cfg/coco.data cfg/yolov4.cfg yolov4.weights http://192.168.0.80:8080/video?dummy=param.mjpg - Yolo v4 - save result videofile res.avi:
./darknet detector demo cfg/coco.data cfg/yolov4.cfg yolov4.weights test.mp4 -out_filename res.avi - Yolo v3 Tiny COCO - video:
./darknet detector demo cfg/coco.data cfg/yolov3-tiny.cfg yolov3-tiny.weights test.mp4 - JSON and MJPEG server that allows multiple connections from your soft or Web-browser
ip-address:8070and 8090:./darknet detector demo ./cfg/coco.data ./cfg/yolov3.cfg ./yolov3.weights test50.mp4 -json_port 8070 -mjpeg_port 8090 -ext_output - Yolo v3 Tiny on GPU #1:
./darknet detector demo cfg/coco.data cfg/yolov3-tiny.cfg yolov3-tiny.weights -i 1 test.mp4 - Alternative method Yolo v3 COCO - image:
./darknet detect cfg/yolov4.cfg yolov4.weights -i 0 -thresh 0.25 - Train on Amazon EC2, to see mAP & Loss-chart using URL like:
http://ec2-35-160-228-91.us-west-2.compute.amazonaws.com:8090in the Chrome/Firefox (Darknet should be compiled with OpenCV):./darknet detector train cfg/coco.data yolov4.cfg yolov4.conv.137 -dont_show -mjpeg_port 8090 -map - 186 MB Yolo9000 - image:
./darknet detector test cfg/combine9k.data cfg/yolo9000.cfg yolo9000.weights - Remember to put data/9k.tree and data/coco9k.map under the same folder of your app if you use the cpp api to build an app
- To process a list of images
data/train.txtand save results of detection toresult.jsonfile use:./darknet detector test cfg/coco.data cfg/yolov4.cfg yolov4.weights -ext_output -dont_show -out result.json < data/train.txt - To process a list of images
data/train.txtand save results of detection toresult.txtuse:./darknet detector test cfg/coco.data cfg/yolov4.cfg yolov4.weights -dont_show -ext_output < data/train.txt > result.txt - Pseudo-labelling - to process a list of images
data/new_train.txtand save results of detection in Yolo training format for each image as label<image_name>.txt(in this way you can increase the amount of training data) use:./darknet detector test cfg/coco.data cfg/yolov4.cfg yolov4.weights -thresh 0.25 -dont_show -save_labels < data/new_train.txt - To calculate anchors:
./darknet detector calc_anchors data/obj.data -num_of_clusters 9 -width 416 -height 416 - To check accuracy mAP@IoU=50:
./darknet detector map data/obj.data yolo-obj.cfg backup\yolo-obj_7000.weights - To check accuracy mAP@IoU=75:
./darknet detector map data/obj.data yolo-obj.cfg backup\yolo-obj_7000.weights -iou_thresh 0.75
For using network video-camera mjpeg-stream with any Android smartphone
-
Download for Android phone mjpeg-stream soft: IP Webcam / Smart WebCam
- Smart WebCam - preferably: https://play.google.com/store/apps/details?id=com.acontech.android.SmartWebCam2
- IP Webcam: https://play.google.com/store/apps/details?id=com.pas.webcam
-
Connect your Android phone to computer by WiFi (through a WiFi-router) or USB
-
Start Smart WebCam on your phone
-
Replace the address below, on shown in the phone application (Smart WebCam) and launch:
- Yolo v4 COCO-model:
./darknet detector demo data/coco.data yolov4.cfg yolov4.weights http://192.168.0.80:8080/video?dummy=param.mjpg -i 0
How to compile on Linux/macOS (using CMake)
The CMakeLists.txt will attempt to find installed optional dependencies like CUDA, cudnn, ZED and build against those. It will also create a shared object library file to use darknet for code development.
To update CMake on Ubuntu, it's better to follow guide here: https://apt.kitware.com/ or https://cmake.org/download/
git clone https://github.com/AlexeyAB/darknet
cd darknet
mkdir build_release
cd build_release
cmake ..
cmake --build . --target install --parallel 8
Using also PowerShell
Install: Cmake, CUDA, cuDNN How to install dependencies
Install powershell for your OS (Linux or MacOS) (guide here).
Open PowerShell type these commands
git clone https://github.com/AlexeyAB/darknet
cd darknet
./build.ps1 -UseVCPKG -EnableOPENCV -EnableCUDA -EnableCUDNN
- remove options like
-EnableCUDAor-EnableCUDNNif you are not interested into - remove option
-UseVCPKGif you plan to manually provide OpenCV library to darknet or if you do not want to enable OpenCV integration - add option
-EnableOPENCV_CUDAif you want to build OpenCV with CUDA support - very slow to build! (requires-UseVCPKG)
If you open the build.ps1 script at the beginning you will find all available switches.
How to compile on Linux (using make)
Just do make in the darknet directory. (You can try to compile and run it on Google Colab in cloud link (press «Open in Playground» button at the top-left corner) and watch the video link ) Before make, you can set such options in the Makefile: link
GPU=1to build with CUDA to accelerate by using GPU (CUDA should be in/usr/local/cuda)CUDNN=1to build with cuDNN v5-v7 to accelerate training by using GPU (cuDNN should be in/usr/local/cudnn)CUDNN_HALF=1to build for Tensor Cores (on Titan V / Tesla V100 / DGX-2 and later) speedup Detection 3x, Training 2xOPENCV=1to build with OpenCV 4.x/3.x/2.4.x - allows to detect on video files and video streams from network cameras or web-camsDEBUG=1to build debug version of YoloOPENMP=1to build with OpenMP support to accelerate Yolo by using multi-core CPULIBSO=1to build a librarydarknet.soand binary runnable fileuselibthat uses this library. Or you can try to run soLD_LIBRARY_PATH=./:$LD_LIBRARY_PATH ./uselib test.mp4How to use this SO-library from your own code - you can look at C++ example: https://github.com/AlexeyAB/darknet/blob/master/src/yolo_console_dll.cpp or use in such a way:LD_LIBRARY_PATH=./:$LD_LIBRARY_PATH ./uselib data/coco.names cfg/yolov4.cfg yolov4.weights test.mp4ZED_CAMERA=1to build a library with ZED-3D-camera support (should be ZED SDK installed), then runLD_LIBRARY_PATH=./:$LD_LIBRARY_PATH ./uselib data/coco.names cfg/yolov4.cfg yolov4.weights zed_camera- You also need to specify for which graphics card the code is generated. This is done by setting
ARCH=. If you use a never version than CUDA 11 you further need to edit line 20 from Makefile and remove-gencode arch=compute_30,code=sm_30 \as Kepler GPU support was dropped in CUDA 11. You can also drop the generalARCH=and just uncommentARCH=for your graphics card.
How to compile on Windows (using CMake)
Requires:
- MSVC: https://visualstudio.microsoft.com/thank-you-downloading-visual-studio/?sku=Community
- CMake GUI:
Windows win64-x64 Installerhttps://cmake.org/download/ - Download Darknet zip-archive with the latest commit and uncompress it: master.zip
In Windows:
-
Start (button) -> All programs -> CMake -> CMake (gui) ->
-
look at image In CMake: Enter input path to the darknet Source, and output path to the Binaries -> Configure (button) -> Optional platform for generator:
x64-> Finish -> Generate -> Open Project -> -
in MS Visual Studio: Select: x64 and Release -> Build -> Build solution
-
find the executable file
darknet.exein the output path to the binaries you specified
How to compile on Windows (using vcpkg)
This is the recommended approach to build Darknet on Windows.
-
Install Visual Studio 2017 or 2019. In case you need to download it, please go here: Visual Studio Community. Remember to install English language pack, this is mandatory for vcpkg!
-
Install CUDA enabling VS Integration during installation.
-
Open Powershell (Start -> All programs -> Windows Powershell) and type these commands:
Set-ExecutionPolicy unrestricted -Scope CurrentUser -Force
git clone https://github.com/AlexeyAB/darknet
cd darknet
.\build.ps1 -UseVCPKG -EnableOPENCV -EnableCUDA -EnableCUDNN
(add option -EnableOPENCV_CUDA if you want to build OpenCV with CUDA support - very slow to build! - or remove options like -EnableCUDA or -EnableCUDNN if you are not interested in them). If you open the build.ps1 script at the beginning you will find all available switches.
How to train with multi-GPU
-
Train it first on 1 GPU for like 1000 iterations:
darknet.exe detector train cfg/coco.data cfg/yolov4.cfg yolov4.conv.137 -
Then stop and by using partially-trained model
/backup/yolov4_1000.weightsrun training with multigpu (up to 4 GPUs):darknet.exe detector train cfg/coco.data cfg/yolov4.cfg /backup/yolov4_1000.weights -gpus 0,1,2,3
If you get a Nan, then for some datasets better to decrease learning rate, for 4 GPUs set learning_rate = 0,00065 (i.e. learning_rate = 0.00261 / GPUs). In this case also increase 4x times burn_in = in your cfg-file. I.e. use burn_in = 4000 instead of 1000.
https://groups.google.com/d/msg/darknet/NbJqonJBTSY/Te5PfIpuCAAJ
How to train (to detect your custom objects)
(to train old Yolo v2 yolov2-voc.cfg, yolov2-tiny-voc.cfg, yolo-voc.cfg, yolo-voc.2.0.cfg, ... click by the link)
Training Yolo v4 (and v3):
- For training
cfg/yolov4-custom.cfgdownload the pre-trained weights-file (162 MB): yolov4.conv.137 (Google drive mirror yolov4.conv.137 ) - Create file
yolo-obj.cfgwith the same content as inyolov4-custom.cfg(or copyyolov4-custom.cfgtoyolo-obj.cfg)and:
- change line batch to
batch=64 - change line subdivisions to
subdivisions=16 - change line max_batches to (
classes*2000, but not less than number of training images and not less than6000), f.e.max_batches=6000if you train for 3 classes - change line steps to 80% and 90% of max_batches, f.e.
steps=4800,5400 - set network size
width=416 height=416or any value multiple of 32: https://github.com/AlexeyAB/darknet/blob/0039fd26786ab5f71d5af725fc18b3f521e7acfd/cfg/yolov3.cfg#L8-L9 - change line
classes=80to your number of objects in each of 3[yolo]-layers:- https://github.com/AlexeyAB/darknet/blob/0039fd26786ab5f71d5af725fc18b3f521e7acfd/cfg/yolov3.cfg#L610
- https://github.com/AlexeyAB/darknet/blob/0039fd26786ab5f71d5af725fc18b3f521e7acfd/cfg/yolov3.cfg#L696
- https://github.com/AlexeyAB/darknet/blob/0039fd26786ab5f71d5af725fc18b3f521e7acfd/cfg/yolov3.cfg#L783
- change [
filters=255] to filters=(classes + 5)x3 in the 3[convolutional]before each[yolo]layer, keep in mind that it only has to be the last[convolutional]before each of the[yolo]layers.- https://github.com/AlexeyAB/darknet/blob/0039fd26786ab5f71d5af725fc18b3f521e7acfd/cfg/yolov3.cfg#L603
- https://github.com/AlexeyAB/darknet/blob/0039fd26786ab5f71d5af725fc18b3f521e7acfd/cfg/yolov3.cfg#L689
- https://github.com/AlexeyAB/darknet/blob/0039fd26786ab5f71d5af725fc18b3f521e7acfd/cfg/yolov3.cfg#L776
- when using
[Gaussian_yolo]layers, change [filters=57] filters=(classes + 9)x3 in the 3[convolutional]before each[Gaussian_yolo]layer- https://github.com/AlexeyAB/darknet/blob/6e5bdf1282ad6b06ed0e962c3f5be67cf63d96dc/cfg/Gaussian_yolov3_BDD.cfg#L604
- https://github.com/AlexeyAB/darknet/blob/6e5bdf1282ad6b06ed0e962c3f5be67cf63d96dc/cfg/Gaussian_yolov3_BDD.cfg#L696
- https://github.com/AlexeyAB/darknet/blob/6e5bdf1282ad6b06ed0e962c3f5be67cf63d96dc/cfg/Gaussian_yolov3_BDD.cfg#L789
So if classes=1 then should be filters=18. If classes=2 then write filters=21. (Do not write in the cfg-file: filters=(classes + 5)x3)
(Generally filters depends on the classes, coords and number of masks, i.e. filters=(classes + coords + 1)*<number of mask>, where mask is indices of anchors. If mask is absence, then filters=(classes + coords + 1)*num)
So for example, for 2 objects, your file yolo-obj.cfg should differ from yolov4-custom.cfg in such lines in each of 3 [yolo]-layers:
[convolutional]
filters=21
[region]
classes=2
- Create file
obj.namesin the directorybuild\darknet\x64\data\, with objects names - each in new line - Create file
obj.datain the directorybuild\darknet\x64\data\, containing (where classes = number of objects):
classes = 2
train = data/train.txt
valid = data/test.txt
names = data/obj.names
backup = backup/
- Put image-files (.jpg) of your objects in the directory
build\darknet\x64\data\obj\ - You should label each object on images from your dataset. Use this visual GUI-software for marking bounded boxes of objects and generating annotation files for Yolo v2 & v3: https://github.com/AlexeyAB/Yolo_mark
It will create .txt-file for each .jpg-image-file - in the same directory and with the same name, but with .txt-extension, and put to file: object number and object coordinates on this image, for each object in new line:
<object-class> <x_center> <y_center> <width> <height>
Where:
-
<object-class>- integer object number from0to(classes-1) -
<x_center> <y_center> <width> <height>- float values relative to width and height of image, it can be equal from(0.0 to 1.0] -
for example:
<x> = <absolute_x> / <image_width>or<height> = <absolute_height> / <image_height> -
attention:
<x_center> <y_center>- are center of rectangle (are not top-left corner)For example for
img1.jpgyou will be createdimg1.txtcontaining:1 0.716797 0.395833 0.216406 0.147222 0 0.687109 0.379167 0.255469 0.158333 1 0.420312 0.395833 0.140625 0.166667
- Create file
train.txtin directorybuild\darknet\x64\data\, with filenames of your images, each filename in new line, with path relative todarknet.exe, for example containing:
data/obj/img1.jpg
data/obj/img2.jpg
data/obj/img3.jpg
-
Download pre-trained weights for the convolutional layers and put to the directory
build\darknet\x64- for
yolov4.cfg,yolov4-custom.cfg(162 MB): yolov4.conv.137 (Google drive mirror yolov4.conv.137 ) - for
yolov4-tiny.cfg,yolov4-tiny-3l.cfg,yolov4-tiny-custom.cfg(19 MB): yolov4-tiny.conv.29 - for
csresnext50-panet-spp.cfg(133 MB): csresnext50-panet-spp.conv.112 - for
yolov3.cfg, yolov3-spp.cfg(154 MB): darknet53.conv.74 - for
yolov3-tiny-prn.cfg , yolov3-tiny.cfg(6 MB): yolov3-tiny.conv.11 - for
enet-coco.cfg (EfficientNetB0-Yolov3)(14 MB): enetb0-coco.conv.132
- for
-
Start training by using the command line:
darknet.exe detector train data/obj.data yolo-obj.cfg yolov4.conv.137To train on Linux use command:
./darknet detector train data/obj.data yolo-obj.cfg yolov4.conv.137(just use./darknetinstead ofdarknet.exe)- (file
yolo-obj_last.weightswill be saved to thebuild\darknet\x64\backup\for each 100 iterations) - (file
yolo-obj_xxxx.weightswill be saved to thebuild\darknet\x64\backup\for each 1000 iterations) - (to disable Loss-Window use
darknet.exe detector train data/obj.data yolo-obj.cfg yolov4.conv.137 -dont_show, if you train on computer without monitor like a cloud Amazon EC2) - (to see the mAP & Loss-chart during training on remote server without GUI, use command
darknet.exe detector train data/obj.data yolo-obj.cfg yolov4.conv.137 -dont_show -mjpeg_port 8090 -mapthen open URLhttp://ip-address:8090in Chrome/Firefox browser)
- (file
8.1. For training with mAP (mean average precisions) calculation for each 4 Epochs (set valid=valid.txt or train.txt in obj.data file) and run: darknet.exe detector train data/obj.data yolo-obj.cfg yolov4.conv.137 -map
-
After training is complete - get result
yolo-obj_final.weightsfrom pathbuild\darknet\x64\backup\- After each 100 iterations you can stop and later start training from this point. For example, after 2000 iterations you can stop training, and later just start training using:
darknet.exe detector train data/obj.data yolo-obj.cfg backup\yolo-obj_2000.weights
(in the original repository https://github.com/pjreddie/darknet the weights-file is saved only once every 10 000 iterations
if(iterations > 1000))- Also you can get result earlier than all 45000 iterations.
- After each 100 iterations you can stop and later start training from this point. For example, after 2000 iterations you can stop training, and later just start training using:
Note: If during training you see nan values for avg (loss) field - then training goes wrong, but if nan is in some other lines - then training goes well.
Note: If you changed width= or height= in your cfg-file, then new width and height must be divisible by 32.
Note: After training use such command for detection: darknet.exe detector test data/obj.data yolo-obj.cfg yolo-obj_8000.weights
Note: if error Out of memory occurs then in .cfg-file you should increase subdivisions=16, 32 or 64: link
How to train tiny-yolo (to detect your custom objects)
Do all the same steps as for the full yolo model as described above. With the exception of:
- Download file with the first 29-convolutional layers of yolov4-tiny: https://github.com/AlexeyAB/darknet/releases/download/darknet_yolo_v4_pre/yolov4-tiny.conv.29 (Or get this file from yolov4-tiny.weights file by using command:
darknet.exe partial cfg/yolov4-tiny-custom.cfg yolov4-tiny.weights yolov4-tiny.conv.29 29 - Make your custom model
yolov4-tiny-obj.cfgbased oncfg/yolov4-tiny-custom.cfginstead ofyolov4.cfg - Start training:
darknet.exe detector train data/obj.data yolov4-tiny-obj.cfg yolov4-tiny.conv.29
For training Yolo based on other models (DenseNet201-Yolo or ResNet50-Yolo), you can download and get pre-trained weights as showed in this file: https://github.com/AlexeyAB/darknet/blob/master/build/darknet/x64/partial.cmd If you made you custom model that isn't based on other models, then you can train it without pre-trained weights, then will be used random initial weights.
When should I stop training
Usually sufficient 2000 iterations for each class(object), but not less than number of training images and not less than 6000 iterations in total. But for a more precise definition when you should stop training, use the following manual:
- During training, you will see varying indicators of error, and you should stop when no longer decreases 0.XXXXXXX avg:
Region Avg IOU: 0.798363, Class: 0.893232, Obj: 0.700808, No Obj: 0.004567, Avg Recall: 1.000000, count: 8 Region Avg IOU: 0.800677, Class: 0.892181, Obj: 0.701590, No Obj: 0.004574, Avg Recall: 1.000000, count: 8
9002: 0.211667, 0.60730 avg, 0.001000 rate, 3.868000 seconds, 576128 images Loaded: 0.000000 seconds
-
9002 - iteration number (number of batch)
-
0.60730 avg - average loss (error) - the lower, the better
When you see that average loss 0.xxxxxx avg no longer decreases at many iterations then you should stop training. The final average loss can be from
0.05(for a small model and easy dataset) to3.0(for a big model and a difficult dataset).Or if you train with flag
-mapthen you will see mAP indicatorLast accuracy [email protected] = 18.50%in the console - this indicator is better than Loss, so train while mAP increases.
- Once training is stopped, you should take some of last
.weights-files fromdarknet\build\darknet\x64\backupand choose the best of them:
For example, you stopped training after 9000 iterations, but the best result can give one of previous weights (7000, 8000, 9000). It can happen due to over-fitting. Over-fitting - is case when you can detect objects on images from training-dataset, but can't detect objects on any others images. You should get weights from Early Stopping Point:
To get weights from Early Stopping Point:
2.1. At first, in your file obj.data you must specify the path to the validation dataset valid = valid.txt (format of valid.txt as in train.txt), and if you haven't validation images, just copy data\train.txt to data\valid.txt.
2.2 If training is stopped after 9000 iterations, to validate some of previous weights use this commands:
(If you use another GitHub repository, then use darknet.exe detector recall... instead of darknet.exe detector map...)
darknet.exe detector map data/obj.data yolo-obj.cfg backup\yolo-obj_7000.weightsdarknet.exe detector map data/obj.data yolo-obj.cfg backup\yolo-obj_8000.weightsdarknet.exe detector map data/obj.data yolo-obj.cfg backup\yolo-obj_9000.weights
And compare last output lines for each weights (7000, 8000, 9000):
Choose weights-file with the highest mAP (mean average precision) or IoU (intersect over union)
For example, bigger mAP gives weights yolo-obj_8000.weights - then use this weights for detection.
Or just train with -map flag:
darknet.exe detector train data/obj.data yolo-obj.cfg yolov4.conv.137 -map
So you will see mAP-chart (red-line) in the Loss-chart Window. mAP will be calculated for each 4 Epochs using valid=valid.txt file that is specified in obj.data file (1 Epoch = images_in_train_txt / batch iterations)
(to change the max x-axis value - change max_batches= parameter to 2000*classes, f.e. max_batches=6000 for 3 classes)
Example of custom object detection: darknet.exe detector test data/obj.data yolo-obj.cfg yolo-obj_8000.weights
-
IoU (intersect over union) - average intersect over union of objects and detections for a certain threshold = 0.24
-
mAP (mean average precision) - mean value of
average precisionsfor each class, whereaverage precisionis average value of 11 points on PR-curve for each possible threshold (each probability of detection) for the same class (Precision-Recall in terms of PascalVOC, where Precision=TP/(TP+FP) and Recall=TP/(TP+FN) ), page-11: http://homepages.inf.ed.ac.uk/ckiw/postscript/ijcv_voc09.pdf
mAP is default metric of precision in the PascalVOC competition, this is the same as AP50 metric in the MS COCO competition. In terms of Wiki, indicators Precision and Recall have a slightly different meaning than in the PascalVOC competition, but IoU always has the same meaning.
Custom object detection
Example of custom object detection: darknet.exe detector test data/obj.data yolo-obj.cfg yolo-obj_8000.weights
 |
 |
|---|
How to improve object detection
- Before training:
-
set flag
random=1in your.cfg-file - it will increase precision by training Yolo for different resolutions: link -
increase network resolution in your
.cfg-file (height=608,width=608or any value multiple of 32) - it will increase precision -
check that each object that you want to detect is mandatory labeled in your dataset - no one object in your data set should not be without label. In the most training issues - there are wrong labels in your dataset (got labels by using some conversion script, marked with a third-party tool, ...). Always check your dataset by using: https://github.com/AlexeyAB/Yolo_mark
-
my Loss is very high and mAP is very low, is training wrong? Run training with
-show_imgsflag at the end of training command, do you see correct bounded boxes of objects (in windows or in filesaug_...jpg)? If no - your training dataset is wrong. -
for each object which you want to detect - there must be at least 1 similar object in the Training dataset with about the same: shape, side of object, relative size, angle of rotation, tilt, illumination. So desirable that your training dataset include images with objects at different: scales, rotations, lightings, from different sides, on different backgrounds - you should preferably have 2000 different images for each class or more, and you should train
2000*classesiterations or more -
desirable that your training dataset include images with non-labeled objects that you do not want to detect - negative samples without bounded box (empty
.txtfiles) - use as many images of negative samples as there are images with objects -
What is the best way to mark objects: label only the visible part of the object, or label the visible and overlapped part of the object, or label a little more than the entire object (with a little gap)? Mark as you like - how would you like it to be detected.
-
for training with a large number of objects in each image, add the parameter
max=200or higher value in the last[yolo]-layer or[region]-layer in your cfg-file (the global maximum number of objects that can be detected by YoloV3 is0,0615234375*(width*height)where are width and height are parameters from[net]section in cfg-file) -
for training for small objects (smaller than 16x16 after the image is resized to 416x416) - set
layers = 23instead of https://github.com/AlexeyAB/darknet/blob/6f718c257815a984253346bba8fb7aa756c55090/cfg/yolov4.cfg#L895 -
for training for both small and large objects use modified models:
- Full-model: 5 yolo layers: https://raw.githubusercontent.com/AlexeyAB/darknet/master/cfg/yolov3_5l.cfg
- Tiny-model: 3 yolo layers: https://raw.githubusercontent.com/AlexeyAB/darknet/master/cfg/yolov4-tiny_3l.cfg
- YOLOv4: 3 yolo layers: https://raw.githubusercontent.com/AlexeyAB/darknet/master/cfg/yolov4-custom.cfg
-
If you train the model to distinguish Left and Right objects as separate classes (left/right hand, left/right-turn on road signs, ...) then for disabling flip data augmentation - add
flip=0here: https://github.com/AlexeyAB/darknet/blob/3d2d0a7c98dbc8923d9ff705b81ff4f7940ea6ff/cfg/yolov3.cfg#L17 -
General rule - your training dataset should include such a set of relative sizes of objects that you want to detect:
train_network_width * train_obj_width / train_image_width ~= detection_network_width * detection_obj_width / detection_image_widthtrain_network_height * train_obj_height / train_image_height ~= detection_network_height * detection_obj_height / detection_image_height
I.e. for each object from Test dataset there must be at least 1 object in the Training dataset with the same class_id and about the same relative size:
object width in percent from Training dataset~=object width in percent from Test datasetThat is, if only objects that occupied 80-90% of the image were present in the training set, then the trained network will not be able to detect objects that occupy 1-10% of the image.
-
to speedup training (with decreasing detection accuracy) set param
stopbackward=1for layer-136 in cfg-file -
each:
model of object, side, illumination, scale, each 30 gradof the turn and inclination angles - these are different objects from an internal perspective of the neural network. So the more different objects you want to detect, the more complex network model should be used. -
to make the detected bounded boxes more accurate, you can add 3 parameters
ignore_thresh = .9 iou_normalizer=0.5 iou_loss=giouto each[yolo]layer and train, it will increase [email protected], but decrease [email protected]. -
Only if you are an expert in neural detection networks - recalculate anchors for your dataset for
widthandheightfrom cfg-file:darknet.exe detector calc_anchors data/obj.data -num_of_clusters 9 -width 416 -height 416then set the same 9anchorsin each of 3[yolo]-layers in your cfg-file. But you should change indexes of anchorsmasks=for each [yolo]-layer, so for YOLOv4 the 1st-[yolo]-layer has anchors smaller than 30x30, 2nd smaller than 60x60, 3rd remaining, and vice versa for YOLOv3. Also you should change thefilters=(classes + 5)*<number of mask>before each [yolo]-layer. If many of the calculated anchors do not fit under the appropriate layers - then just try using all the default anchors.
- After training - for detection:
-
Increase network-resolution by set in your
.cfg-file (height=608andwidth=608) or (height=832andwidth=832) or (any value multiple of 32) - this increases the precision and makes it possible to detect small objects: link -
it is not necessary to train the network again, just use
.weights-file already trained for 416x416 resolution -
to get even greater accuracy you should train with higher resolution 608x608 or 832x832, note: if error
Out of memoryoccurs then in.cfg-file you should increasesubdivisions=16, 32 or 64: link
How to mark bounded boxes of objects and create annotation files
Here you can find repository with GUI-software for marking bounded boxes of objects and generating annotation files for Yolo v2 - v4: https://github.com/AlexeyAB/Yolo_mark
With example of: train.txt, obj.names, obj.data, yolo-obj.cfg, air1-6.txt, bird1-4.txt for 2 classes of objects (air, bird) and train_obj.cmd with example how to train this image-set with Yolo v2 - v4
Different tools for marking objects in images:
- in C++: https://github.com/AlexeyAB/Yolo_mark
- in Python: https://github.com/tzutalin/labelImg
- in Python: https://github.com/Cartucho/OpenLabeling
- in C++: https://www.ccoderun.ca/darkmark/
- in JavaScript: https://github.com/opencv/cvat
- in C++: https://github.com/jveitchmichaelis/deeplabel
- in C#: https://github.com/BMW-InnovationLab/BMW-Labeltool-Lite
- DL-Annotator for Windows ($30): url
- v7labs - the greatest cloud labeling tool ($1.5 per hour): https://www.v7labs.com/
How to use Yolo as DLL and SO libraries
- on Linux
- using
build.shor - build
darknetusingcmakeor - set
LIBSO=1in theMakefileand domake
- using
- on Windows
- using
build.ps1or - build
darknetusingcmakeor - compile
build\darknet\yolo_cpp_dll.slnsolution orbuild\darknet\yolo_cpp_dll_no_gpu.slnsolution
- using
There are 2 APIs:
-
C API: https://github.com/AlexeyAB/darknet/blob/master/include/darknet.h
- Python examples using the C API:
-
C++ API: https://github.com/AlexeyAB/darknet/blob/master/include/yolo_v2_class.hpp
- C++ example that uses C++ API: https://github.com/AlexeyAB/darknet/blob/master/src/yolo_console_dll.cpp
-
To compile Yolo as C++ DLL-file
yolo_cpp_dll.dll- open the solutionbuild\darknet\yolo_cpp_dll.sln, set x64 and Release, and do the: Build -> Build yolo_cpp_dll- You should have installed CUDA 10.2
- To use cuDNN do: (right click on project) -> properties -> C/C++ -> Preprocessor -> Preprocessor Definitions, and add at the beginning of line:
CUDNN;
-
To use Yolo as DLL-file in your C++ console application - open the solution
build\darknet\yolo_console_dll.sln, set x64 and Release, and do the: Build -> Build yolo_console_dll-
you can run your console application from Windows Explorer
build\darknet\x64\yolo_console_dll.exeuse this command:yolo_console_dll.exe data/coco.names yolov4.cfg yolov4.weights test.mp4 -
after launching your console application and entering the image file name - you will see info for each object:
<obj_id> <left_x> <top_y> <width> <height> <probability> -
to use simple OpenCV-GUI you should uncomment line
//#define OPENCVinyolo_console_dll.cpp-file: link -
you can see source code of simple example for detection on the video file: link
-
yolo_cpp_dll.dll-API: link
struct bbox_t {
unsigned int x, y, w, h; // (x,y) - top-left corner, (w, h) - width & height of bounded box
float prob; // confidence - probability that the object was found correctly
unsigned int obj_id; // class of object - from range [0, classes-1]
unsigned int track_id; // tracking id for video (0 - untracked, 1 - inf - tracked object)
unsigned int frames_counter;// counter of frames on which the object was detected
};
class Detector {
public:
Detector(std::string cfg_filename, std::string weight_filename, int gpu_id = 0);
~Detector();
std::vector<bbox_t> detect(std::string image_filename, float thresh = 0.2, bool use_mean = false);
std::vector<bbox_t> detect(image_t img, float thresh = 0.2, bool use_mean = false);
static image_t load_image(std::string image_filename);
static void free_image(image_t m);
#ifdef OPENCV
std::vector<bbox_t> detect(cv::Mat mat, float thresh = 0.2, bool use_mean = false);
std::shared_ptr<image_t> mat_to_image_resize(cv::Mat mat) const;
#endif
};
Citation
@misc{bochkovskiy2020yolov4,
title={YOLOv4: Optimal Speed and Accuracy of Object Detection},
author={Alexey Bochkovskiy and Chien-Yao Wang and Hong-Yuan Mark Liao},
year={2020},
eprint={2004.10934},
archivePrefix={arXiv},
primaryClass={cs.CV}
}
@InProceedings{Wang_2021_CVPR,
author = {Wang, Chien-Yao and Bochkovskiy, Alexey and Liao, Hong-Yuan Mark},
title = {{Scaled-YOLOv4}: Scaling Cross Stage Partial Network},
booktitle = {Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)},
month = {June},
year = {2021},
pages = {13029-13038}
}























